Chapter

Coordinate geometry (Rekha Ganit) including the proof of Pythagoras theorem are provided below.

Part A

Pythagoras theorem states that in a right angle triangle, the square of hypotenuse is equal to the sum of the square of the other two sides

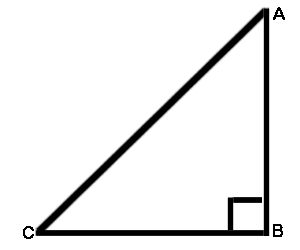
In the right angle Triangle ABC

In Vedic Maths, a very simple proof of Pythagoras Theorem is given and it was proved much earlier (earlier than the birth of Pythagoras !)

It is described here and it involves the construction of this geometrical figure

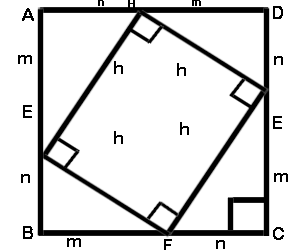
Here we have to construct a square ABCD and a smaller square EFGH inside it such that

Now we know that Area of Square = (sides)² and Area of  Triangle x base x height using these.

Area of square 

Area of square

Area of the 4 triangles(.................)

Now  Area of sqr. ABCD= Area of sqr. EFGH + Area of 4

Substituting

or 

This proves Pythagoras theorem 

as

hypotheses

We have proved

or 

in the right angle Triangle EBF which is the required proof of Pythagoras Theorem

which is the required proof of Pythagoras Theorem

Part B

Rekha Ganit or the Coordinate Geometry gives us the equation of a straight line passing through two given points A and B having coordinate A(a,b) and B(c,d)

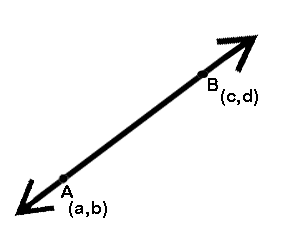
The equation of straight line AB is given by the following equation

Example 1

Find the equation of straight line passing through 2 points A(9,17) and B(7,-2) here a=9 , b=17 , c=7 , d=-2 putting in the equation

or

or is the required equation of straight line

Exercise

Find the equation of straight line passing through two given points

Exercise                                    Solution