Chapter

This chapter involves the exact calculation of cube root of a perfect cube.  A perfect cube is the cube of a whole number.  For example 12³ = 1728 so the 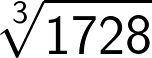  is 12.

For calculating the cube root the cubes of first ten natural numbers (1 to 10) must be memorized:

1³ = 1

2³ = 8

3³ = 27

4³ = 64

5³ = 125

6³ = 216

7³ = 343

8³ = 512

9³ = 729

10³ = 1000

From the above table we can conclude that there is a unique correlation between the unit digit of a perfect cube and its cube root.  The correlation is illustrated in the following table:

Unit Digits of 

Cube      Cube Root

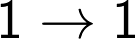
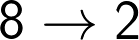
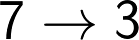
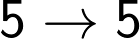
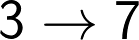
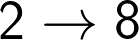
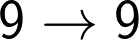
In Other words six digits 1, 4, 5, 6, 9 and 0 repeat themselves in the cube root and four digits 2, 3, 7 and 8 have an inter-play of complements of 10.  Therefore 2, 3, 7 and 8 change to 8, 7, 3 and 2 respectively in cube root.

Therefore, as soon as you see the unit digit of the given cube, you can make out (determine) the unit digit of the cube root, with the help of the above table.

Example 1:

It is clear that the unit digit of its cube root should be 3

Steps for finding the ten's digit of cube root:

Step 1: Remove three digit from the right of the number 79 507

Step 2: Now refer the remaining no. [79 in this case] to the basic cube chart 64 < 79 < 125  i.e 4³ < 79 < 5³  so 79 lies between 4³ and 5³

Step 3: Now select the smaller of the two cubes (4) and put it in the ten's place.

Step 4: So final answer obtained is 43 

   so within seconds, we can determine the cube root of a perfect cube.

(In this and subsequent examples T = Ten's digit and U = Unit digit)

Example 2: 

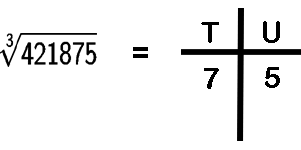
Unit digit is 5

Ten's digit is 7

  7³ <  421 <  8³

Example 3:

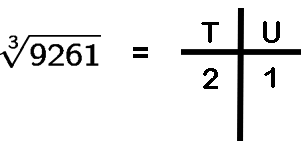
Unit digit is 1

Ten's digit is 2 , as

2³ < 9 < 3³

Example 4:

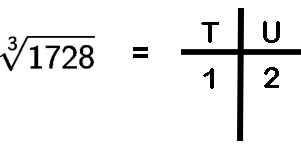
Unit digit of cube root is 2 (corresponding to unit digit 8 of cube)

Ten's digit is 1 (as 1³ = 1)

Example 5:

Exercises:

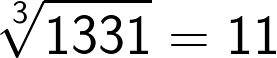
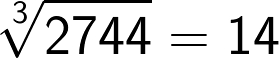
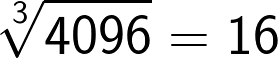
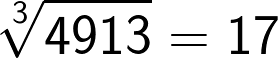
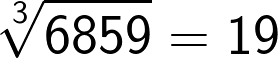
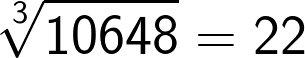
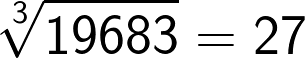
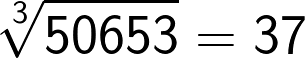
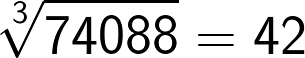
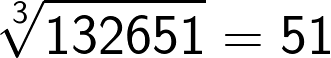
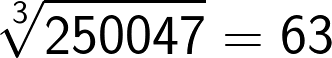
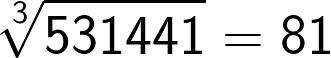
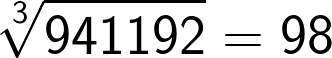
Now if the cube consists of 7 to 9 digit numbers then the cube root will consist of 3 digits.  This method holds good for these large numbers as well.

Example:

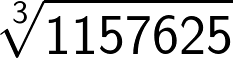
Step 1: Write the unit digit of cube root as 5

Step 2: Remove 3 digits from the right of the number so now 1157 is remaining 

Step 3: We can see that 1157 lies between 10³ (1000) and 11³ (1331) i.e. 10³ < 1157 < 11³

Step 4: So we select 10 as hundred's & ten's digit respectively

Step 5: So final answer obtained is 105.

Exercise: