A number like 10, 100, 1,000 etc..is called a base. A base is considered to be any power of 10. This method is more helpful when the numbers to be multiplied are close to the same base.
There are three types in this method:
- Type A: When both the numbers are higher than the base.
- Type B: When both the numbers are lower than the base.
- Type C: When one of the numbers is higher than the base and the other is lower than the base
Type A: When both the numbers are higher than the base as in Example 1 below.
Example: 12 x 13
Step 1: Select a base which is closest to both the numbers. Here we would select the base 10.
Step 2: Find the difference between the two numbers and the base and write the respective difference in front of the numbers, with its proper sign (+ve or -ve)
12 - 10 = +2 and 13 - 10 = +3 Therefore you would write:
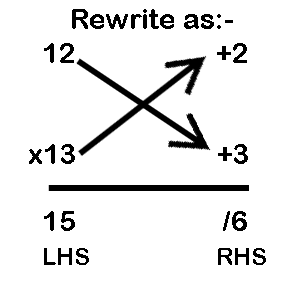
Answer = 156
Step 3: Multiply the differences (+2 and +3) and write the product 6 in the RHS of the answer
Step 4: Cross add the difference to any one of the numbers and write the sum on the LHS of the answer (12 + 3 or 13 + 2) is equal to 15. This forms the LHS of the answer.
Step 5: Combine the LHS and RHS to derive the final answer (15 and 6 results in 156).
Example 2: 12 x 14 = 12 + 4/2 x 4
= 16/8
=168
Answer = 210
Example 3: 14 x 15 = 14 + 5/ 4 x 5
= 19/20
= 19+2 (Carried over) / 0
= 210
This example follows the rule of carry over which is critical in this chapter.
Let us elaborate the rule of carry over. The rule of carry over states that the number of digits on the RHS should be exactly equal to the number of zeros in the base. As in this example the base 10 has only one zero so we can keep only one digit (unit digit 0) in the RHS and carry over the tenth digit 2 to LHS and add it to 19.
Example 4: 104 x 109 = (104 + 9)/(4 x 9)
= 113/36
= 11336
Here the base is 100 so RHS contains two digits 36.
Example 5: 102 x 103 = (102 + 3)/(2 x 3)
=105/06
=10506
Important to note that the RHS should contain two digits because the base is 100. That is why we have WRITTEN 06 AND NOT 6 on the RHS.
Example 6: 1011 x 1024 = (1011 + 24)/(11 x 24)
=1035/264
=1035264
Note that here the base is 1,000 and that is why the RHS has three digits.
Example 7: 1008 x 1008 = (1008 + 8)/(8 x 8)
= 1016/064
= 1016064
Exercises:
13 x 14 =182
14 x 16 = 224
17 x 18 = 306
107 x 109 = 11663
111 x 103 = 11433
102 x 104 = 10608
10.1 x 1.12 = 11.312 (Do the sum without decimals and then add the decimals in the resulting answer.
1.05 x 13.2 = 13.86
1011 x 1066 = 1077726
1012 x 1013 = 1025156
1002 x 1006 = 1008012
1008 x 1003 = 1011024
10.11 x 12.13 = 122.6343 (Here the base should be 1,000)
100.2 x 21.14 = 2118.228 (Here the base should be 1,000)
10104 x 10106 = 102111024 (Here the base should be 10,000)
Type B: When both the numbers are lower than the base hence the difference will be a negative number.
Example1: 94 x 97
Step 1: Select the base 100
Step 2: Take the difference (94 - 100 = -6) and (97 – 100 = -3)
Step 3: Write the difference next to the respective numbers:
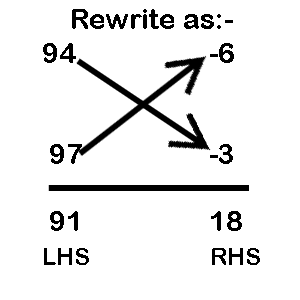
Answer = 9118
Step 4: Multiply the differences (-6 x -3 = 18) and write the product on the RHS
Step 5: Now we need to cross add the difference to any of the two numbers [94 + (-3) = 91) OR (97 + (-6) = 91]. The result 91 comes on the LHS of the answer.
Step 6: Combine the LHS and RHS to obtain the final answer as 9118
The rule of carry over as described above is applicable in this type.
Example 2: 89 x 75 = (89 - 25)/(11 x 25)
= 64/275
= 6675 (Note 2 is carried over from RHS to LHS as the base here is 100)
Example 3: 989 x 986 = (989 - 14)/(11 x 14)
= 975/154
= 975154 (Note the base was 1,000)
Example 4: 997 x 997 = (997 - 3)/(3 x 3)
= 994/009
= 994009 ( Note that we should have 3 digits on the RHS so we had to prefix two zeros before the 9)
Example 5: 98.1 x 99.7 = 981 x 997
= (981 - 3)/(19 x 3)
= 978/057
= 9780.57 (Place the decimal back in the answer at the appropriate place)
Exercises:
92 x 93 = 8556
91 x 88 = 8008
989 x 971 = 960319
989 x 939 = 928671
988 x 992 = 980096
989 x 784 = 775376 (Note the base is 1,000)
998 x 668 = 666664 (Note the base is 1,000)
98.9 x 91.7 = 9069.13
9.97 x 8.87 = 88.4339 (Note the base is 1,000)
9897 x 9891 = 97891227 (Note the base is 10,000)
Type C: When one of the numbers is higher than the base and the other is lower than the base.
Example 1: 104 x 98
Step 1: Taking the base as 100 we see that 104 is higher than 100 and 98 is lower.
Step2: The difference between (104 – 100 = +4) and (98 – 100 = -2)
Step 3: Multiplying the two differences on RHS will result in a negative number
i.e. +4x - 2 = -8
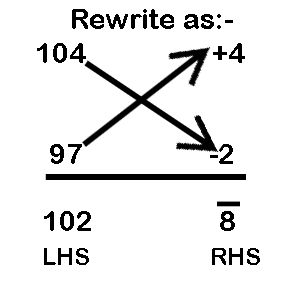
Answer = 10192
102/8 (bar on top) (The bar on the top is called VINCULUM which signifies a negative number).
Step 4: To derive the final answer we need to take the LHS and append the number of zeros equal to the number of zeros in the base and then subtract the RHS from the result.
(10200 – 8 = 10192).
Note: The addition of the zeros to the LHS number and that there is no need to carry over in this type.
Example 2: 108 x 95 = (108-5)/(-40) bar on the top
= 103/-40
= 10300-40
= 10260
Exercises:
109 x 91 = 9919
117 x 88 = 10296
92 x 102 = 9384
18 x 8 = 144
991 x 1001 = 991991
It is interesting to note that in the last exercise 991 x 1001 = 991991, we see that the same three digits are repeated.
So whenever we multiply any three digit number, say abc, by 1001 the product will be abcabc. (Example 786 x 1001 = 786786).
Course:


