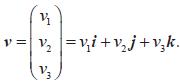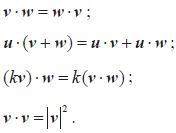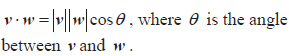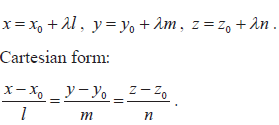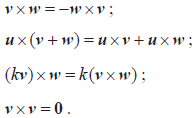| Content | Further guidance | Links | |
| 4.1 |
Concept of a vector. Representation of vectors using directed line segments. Unit vectors; base vectors i, j, k. Components of a vector:
Algebraic and geometric approaches to the following: the sum and difference of two vectors; the zero vectors 0 , the vector −v ; multiplication by a scalar, kv ; magnitude of a vector, |v| ; position vectors
|
Proofs of geometrical properties using vectors. Distance between points A and B is themagnitude of 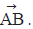 |
|
| 4.2 |
The definition of the scalar product of two vectors. Properties of the scalar product:
The angle between two vectors. Perpendicular vectors; parallel vectors. |
Link to 3.6. For non-zero vectors, v ⋅ w = 0 is equivalent to the vectors being perpendicular. For parallel vectors, |v ⋅w| = |v| |w| . |
|
| 4.3 | Vector equation of a line in two and three dimensions: r = a+ λb . Simple applications to kinematics.The angle between two lines. |
Knowledge of the following forms for equations of lines. Parametric form:
|
|
| 4.4 | Coincident, parallel, intersecting and skew lines; distinguishing between these cases. Points of intersection. | . | . |
| 4.5 |
The definition of the vector product of two vectors. Properties of the vector product:
Geometric interpretation of |v × w| . |
v × w = |v| |w| sinθ n , where θ is the angle between v and w and n is the unit normal vector whose direction is given by the right- hand screw rule. Areas of triangles and parallelograms. |
|
| 4.6 |
Vector equation of a plane r = a +λb + μc . Use of normal vector to obtain the form r ⋅ n = a ⋅ n. Cartesian equation of a plane ax + by + cz = d . |
. | . |
| 4.7 |
Intersections of: a line with a plane; two planes; three planes. Angle between: a line and a plane; two planes. |
Link to 1.9.Geometrical interpretation of solutions. |
|