| |
Content |
Further guidance |
Links |
| 4.1 |
- Vectors as displacements in the plane and in three dimensions.
- Components of a vector; column representation;
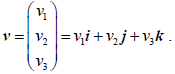
Algebraic and geometric approaches to the following:
- the sum and difference of two vectors; the zero vector, the vector −v ;
- multiplication by a scalar, kv ; parallel vectors;
- magnitude of a vector, |v| ;
- unit vectors; base vectors; i, j and k;
- position vectors

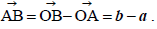
|
- Link to three-dimensional geometry, x, y and z- axes.
- Components are with respect to the unit vectors i, j and k (standard basis).
- Applications to simple geometric figures are essential.
- The difference of v and w is v − w = v + (−w) . Vector sums and differences can be represented by the diagonals of a parallelogram.
- Multiplication by a scalar can be illustrated by enlargement.
- Distance between points A and B is the magnitude of
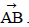
|
- Appl: Physics 1.3.2 (vector sums and differences) Physics 2.2.2, 2.2.3 (vector resultants).
- TOK: How do we relate a theory to the author? Who developed vector analysis: JW Gibbs or O Heaviside?
|
| 4.2 |
- The scalar product of two vectors.
- Perpendicular vectors; parallel vectors.
- The angle between two vectors.
|
- The scalar product is also known as the “dot product”.
- Link to 3.6, cosine rule.
- For non-zero vectors, v w = 0 is equivalent to the vectors being perpendicular For parallel vectors, w = kv , |v ⋅w| = |v| |w| .
|
|
| 4.3 |
Vector equation of a line in two and three dimensions: r = a + tb . |
- Relevance of a (position) and b (direction).
- Interpretation of t as time and b as velocity, with |b| representing speed.
|
- Aim 8: Vector theory is used for tracking displacement of objects, including for peaceful and harmful purposes.
- TOK: Are algebra and geometry two separate domains of knowledge? (Vector algebra is a good opportunity to discuss how geometrical properties are described and generalized by algebraic methods.)
|
| 4.4 |
- Distinguishing between coincident and parallel lines.
- Finding the point of intersection of two lines.
- Determining whether two lines intersect.
|
. |
. |