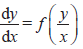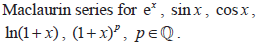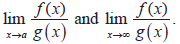| |
Content |
Further guidance |
Links |
| 9.1 |
Infinite sequences of real numbers and their convergence or divergence. |
- Informal treatment of limit of sum, difference, product, quotient; squeeze theorem.
- Divergent is taken to mean not convergent.
|
TOK: Zeno’s paradox, impact of infinite sequences and limits on our understanding of the physical world. |
| 9.2 |
- Convergence of infinite series.
- Tests for convergence: comparison test; limit comparison test; ratio test; integral test.
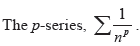 - Series that converge absolutely.
- Series that converge conditionally.
- Alternating series.
- Power series: radius of convergence and interval of convergence. Determination of the radius of convergence by the ratio test.
|
The sum of a series is the limit of the sequence of its partial sums.
Students should be aware that if 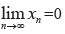 then n the series is not necessarily convergent, but if then n the series is not necessarily convergent, but if 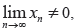 the series diverges. the series diverges.
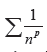 is convergent for p >1 and divergent otherwise. When p = 1, this is the harmonic series. Conditions for convergence. is convergent for p >1 and divergent otherwise. When p = 1, this is the harmonic series. Conditions for convergence.
The absolute value of the truncation error is less than the next term in the series.
|
TOK: Euler’s idea that 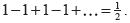 Was it a mistake or just an alternative view? Was it a mistake or just an alternative view? |
| 9.3 |
- Continuity and differentiability of a function at a point.
- Continuous functions and differentiable functions.
|

|
. |
| 9.4 |
- The integral as a limit of a sum; lower and upper Riemann sums.
- Fundamental theorem of calculus.
- Improper integrals of the type.
|
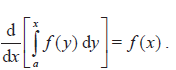 |
- Int: How close was Archimedes to integral calculus?
- Int: Contribution of Arab, Chinese and Indian mathematicians to the development of calculus.
- Aim 8: Leibniz versus Newton versus the “giants” on whose shoulders they stood—who deserves credit for mathematical progress?
- TOK: Consider
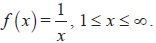
- An infinite area sweeps out a finite volume. Can this be reconciled with our intuition? What does this tell us about mathematical knowledge
? |
| 9.5 |
- First-order differential equations.
- Geometric interpretation using slope fields, including identification of isoclines.
- Numerical solution of
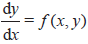 using Euler’s method. using Euler’s method.
- Variables separable.
- Homogeneous differential equation
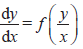
- using the substitution y = vx.
- Solution of y′ + P(x)y = Q(x), using the integrating factor.
|
 |
Appl: Real-life differential equations, eg Newton’s law of cooling,population growth, carbon dating. |
| 9.6 |
- Rolle’s theorem. Mean value theorem.
- Taylor polynomials; the Lagrange form of the error term.
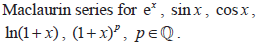 - Use of substitution, products, integration and differentiation to obtain other series.
- Taylor series developed from differential equations.
|
- Applications to the approximation of functions; formula for the error term, in terms of the value of the (n + 1)th derivative at an intermediate point.
- Students should be aware of the intervals of convergence.
|
- Int, TOK: Influence of Bourbaki on understanding and teaching of mathematics.
- Int: Compare with work of the Kerala school.
|
| 9.7 |
The evaluation of limits of the form
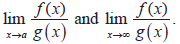
Using l’Hôpital’s rule or the Taylor series.
|
The indeterminate forms 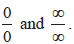 Repeated use of l’Hôpital’s rule. Repeated use of l’Hôpital’s rule. |
. |
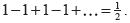 Was it a mistake or just an alternative view?
Was it a mistake or just an alternative view?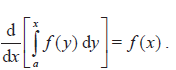

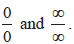 Repeated use of l’Hôpital’s rule.
Repeated use of l’Hôpital’s rule.

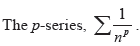
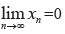 then n the series is not necessarily convergent, but if
then n the series is not necessarily convergent, but if 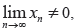 the series diverges.
the series diverges.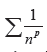 is convergent for p >1 and divergent otherwise. When p = 1, this is the harmonic series. Conditions for convergence.
is convergent for p >1 and divergent otherwise. When p = 1, this is the harmonic series. Conditions for convergence.
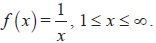
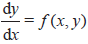 using Euler’s method.
using Euler’s method.