| |
Content |
Further guidance |
Links |
| 8.1 |
- Finite and infinite sets. Subsets.
- Operations on sets: union; intersection; complement; set difference; symmetric difference.
- De Morgan’s laws: distributive, associative and commutative laws (for union and intersection).
|
- Illustration of these laws using Venn diagrams.
- Students may be asked to prove that two sets are the same by establishing that A ⊆ B and B ⊆ A .
|
- TOK: Cantor theory of transfinite numbers, Russell’s paradox, Godel’s incompleteness theorems.
- Appl: Logic, Boolean algebra, computer circuits.
|
| 8.2 |
- Ordered pairs: the Cartesian product of two sets.
- Relations: equivalence relations; equivalence classes.
|
An equivalence relation on a set forms a partition of the set. |
Appl, Int: Scottish clans. |
| 8.3 |
- Functions: injections; surjections; bijections.
- Composition of functions and inverse functions.
|
- The term codomain.
- Knowledge that the function composition is not a commutative operation and that if f is a bijection from set A to set B then f −1 exists and is a bijection from set B to set A.
|
. |
| 8.4 |
- Binary operations.
- Operation tables (Cayley tables).
-
|
- A binary operation on a non-empty set S is a rule for combining any two elements a,b ∈ S to give a unique element c. That is, in this definition, a binary operation on a set is not necessarily closed.
|
|
| 8.5 |
Binary operations: associative, distributive and commutative properties.
|
- The arithmetic operations on R and C
- Examples of distributivity could include the fact that, on R , multiplication is distributive over addition but addition is not distributive over multiplication.
|
TOK: Which are more fundamental, the general models or the familiar examples? |
| 8.6 |
- The identity element e.
- The inverse a−1 of an element a.
- Proof that left-cancellation and right cancellation by an element a hold, provided that a has an inverse.
- Proofs of the uniqueness of the identity and inverse elements.
|
Both the right-identity a ∗ e = a and left- identity e ∗ a = a must hold if e is an identity element.
Both a ∗ a−1 = e and a−1 ∗ a = e must hold.
|
. |
| 8.7 |
- The definition of a group {G,*} .
- The operation table of a group is a Latin square, but the converse is false.
- Abelian groups.
|
For the set G under a given operation * :
- G is closed under * ;
- * is associative;
- G contains an identity element;
- each element in G has an inverse in G.
- a ∗b = b ∗ a , for all a,b∈G .
|
- Appl: Existence of formula for roots of polynomials.
- Appl: Galois theory for the impossibility of such formulae for polynomials of degree 5 or higher.
|
| 8.8 |
Examples of groups:
- R, Q, Z and C under addition;
- integers under addition modulo n;
- non-zero integers under multiplication, modulo p, where p is prime;
symmetries of plane figures, including equilateral triangles and rectangles;
invertible functions under composition of functions.
|
The composition T2oT1 denotes T1 followed by T2 . |
Appl: Rubik’s cube, time measures, crystal structure, symmetries of molecules, strut and cable constructions, Physics H2.2 (special relativity), the 8–fold way, supersymmetry. |
| 8.9 |
- The order of a group.
- The order of a group element.
- Cyclic groups.
- Generators.
- Proof that all cyclic groups are Abelian.
|
. |
Appl: Music circle of fifths, prime numbers. |
| 8.10 |
- Permutations under composition of permutations.
- Cycle notation for permutations.
- Result that every permutation can be written as a composition of disjoint cycles.
- The order of a combination of cycles.
|
On examination papers: the form 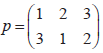 or in cycle notation (132) will be used to represent the permutation. or in cycle notation (132) will be used to represent the permutation.
1-->3, 2-->1, 3-->2
|
Appl: Cryptography, campanology. |
| 8.11 |
- Subgroups, proper subgroups.
- Use and proof of subgroup tests.
- Definition and examples of left and right cosets
- of a subgroup of a group.
- Lagrange’s theorem.
- Use and proof of the result that the order of a finite group is divisible by the order of any element. (Corollary to Lagrange’s theorem.)
|
- A proper subgroup is neither the group itself nor the subgroup containing only the identity element.
- Suppose that {G,∗} is a group and H is a non-empty subset of G. Then {H∗,} is a subgroup of {G,∗} if a b−1 ∈ H whenever a,b ∈ H .
- Suppose that {G,∗} is a finite group and H is a non-empty subset of G. Then {H,∗} is a subgroup of {G,∗} if H is closed under ∗ .
|
Appl: Prime factorization, symmetry breaking. |
| 8.12 |
- Definition of a group homomorphism.
- Definition of the kernel of a homomorphism. Proof that the kernel and range of a homomorphism are subgroups.
- Proof of homomorphism properties for identities and inverses.
- Isomorphism of groups.
- The order of an element is unchanged by an isomorphism.
|
Infinite groups as well as finite groups.
Let {G,*} and {H,o} be groups, then the
function f :G→H is a homomorphism if
f (a *b) = f (a)o f (b) for all a,b∈G .
If f :G→H is a group homomorphism, then
Ker( f ) is the set of a∈G such that
f (a) = eH .
Identity: let eG and eH be the identity elements
of (G,∗) and (H,o) , respectively, then
f (eG )= eH .
Inverse: f (a-1) = ( f (a)) -1 for all a∈G .
Infinite groups as well as finite groups.
The homomorphism f :G→H is an
isomorphism if f is bijective.
I
|
|


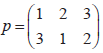 or in cycle notation (132) will be used to represent the permutation.
or in cycle notation (132) will be used to represent the permutation.