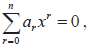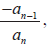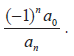| |
Content |
Further guidance |
Links |
| 2.1 |
Concept of function f : x--> f (x) : domain,
range; image (value).
Odd and even functions.
Composite functions f ° g .
Identity function.
One-to-one and many-to-one functions.
Inverse function f −1 , including domain restriction. Self-inverse functions. |
( f ° g)(x) = f (g(x)) .Link with 6.2.
Link with 3.4.
Link with 6.2. |
- Int: The notation for functions was developed by a number of different mathematicians in the 17th and 18th centuries. How did the notation we use today become internationally accepted?
- TOK: The nature of mathematics. Is mathematics simply the manipulation of symbols under a set of formal rules?
|
| 2.2 |
- The graph of a function; its equation y = f (x) .
- Investigation of key features of graphs, such as maximum and minimum values, intercepts, horizontal and vertical asymptotes and symmetry, and consideration of domain and range.
- The graphs of the functions y =| f (x) | and y = f ( x ).
- The graph of
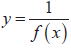 given the graph of y = f ( x ) given the graph of y = f ( x )
|
- Use of technology to graph a variety of functions.
|
- TOK: Mathematics and knowledge claims. Does studying the graph of a function contain the same level of mathematical rigour as studying the function algebraically (analytically)?
- Appl: Sketching and interpreting graphs;Geography SL/HL (geographic skills); Chemistry 11.3.1.
- Int: Bourbaki group analytical approach versus Mandlebrot visual approach.
|
| 2.3 |
- Transformations of graphs: translations; stretches; reflections in the axes.
- The graph of the inverse function as a reflection in y = x .
|
Link to 3.4. Students are expected to be aware of the effect of transformations on both the algebraic expression and the graph of a function. |
Appl: Economics SL/HL 1.1 (shift in demand and supply curves). |
| 2.4 |
- The rational function
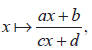 and its graph. and its graph.
- The function
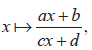 and its graph. and its graph.
- The function
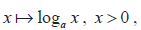 and its graph. and its graph.
|
- The reciprocal function is a particular case.
- Graphs should include both asymptotes and any intercepts with axes.
- Exponential and logarithmic functions as inverses of each other.
- Link to 6.2 and the significance of e.
- Application of concepts in 2.1, 2.2 and 2.3
. |
Appl: Geography SL/HL (geographic skills); Physics SL/HL 7.2 (radioactive decay);Chemistry SL/HL 16.3 (activation energy); Economics SL/HL 3.2 (exchange rates). |
| 2.5 |
- Polynomial functions and their graphs.
- The factor and remainder theorems.
- The fundamental theorem of algebra
|
- The graphical significance of repeated factors.
- The relationship between the degree of a polynomial function and the possible numbers of x-intercepts.
|
. |
| 2.6 |
- Solving quadratic equations using the quadratic formula.
- Use of the discriminant ∆ = b2 − 4ac to determine the nature of the roots.
- Solving polynomial equations both graphically and algebraically.
- Sum and product of the roots of polynomial equations.
- Solution of ax = b using logarithms.
- Use of technology to solve a variety of equations, including those where there is no appropriate analytic approach.
|
- May be referred to as roots of equations or zeros of functions.
- Link the solution of polynomial equations to conjugate roots in 1.8.
- For the polynomial equation
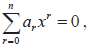
- the sum is
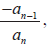
- the product is
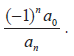
|
- Appl: Chemistry 17.2 (equilibrium law).
- Appl: Physics 2.1 (kinematics).
- Appl: Physics 4.2 (energy changes in simple harmonic motion).
- Appl: Physics (HL only) 9.1 (projectile motion).
- Aim 8: The phrase “exponential growth” is used popularly to describe a number of phenomena. Is this a misleading use of a mathematical term?
|
| 2.7 |
- Solutions of g(x) ≥ f (x) .
- Graphical or algebraic methods, for simple polynomials up to degree 3.
- Use of technology for these and other functions.
|
. |
. |


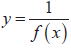 given the graph of y = f ( x )
given the graph of y = f ( x )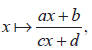 and its graph.
and its graph.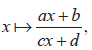 and its graph.
and its graph.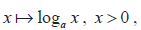 and its graph.
and its graph.