| |
Content |
Further guidance |
Links |
| 1.1 |
Arithmetic sequences and series; sum of finite arithmetic series; geometric sequences and series; sum of finite and infinite geometric series. Sigma notation. Applications. |
Sequences can be generated and displayed in several ways, including recursive functions. Link infinite geometric series with limits of convergence in 6.1. Examples include compound interest and population growth. |
- Int: The chess legend (Sissa ibn Dahir).
- Int: Aryabhatta is sometimes considered the “father of algebra”. Compare with al-Khawarizmi.
- Int: The use of several alphabets in mathematical notation (eg first term and common difference of an arithmetic sequence).
- TOK: Mathematics and the knower. To what extent should mathematical knowledge be consistent with our intuition?
- TOK: Mathematics and the world. Some mathematical constants ( π , e, φ , Fibonacci numbers) appear consistently in nature. What does this tell us about mathematical knowledge?
- TOK: Mathematics and the knower. How is mathematical intuition used as a basis for formal proof? (Gauss’ method for adding up integers from 1 to 100.)
- Aim 8: Short-term loans at high interest rates. How can knowledge of mathematics result in individuals being exploited or protected from extortion?
- Appl: Physics 7.2, 13.2 (radioactive decay and nuclear physics).
|
| 1.2 |
- Exponents and logarithms.
- Laws of exponents; laws of logarithms.
- Change of base.
|
Exponents and logarithms are further developed in 2.4. |
- Appl: Chemistry 18.1, 18.2 (calculation of pH and buffer solutions).
- TOK: The nature of mathematics and science. Were logarithms an invention or discovery? (This topic is an opportunity for teachers and students to reflect on “the nature of mathematics”.)
|
| 1.3 |
Counting principles, including permutations and combinations.
The binomial theorem: expansion of (a + b)n , n ∈ N
Not required:
- Permutations where some objects are identical.
- Circular arrangements.
- Proof of binomial theorem.
|
The ability to find  using both the formula and technology is expected. Link to 5.4. using both the formula and technology is expected. Link to 5.4.
Link to 5.6, binomial distribution. .
|
- TOK: The nature of mathematics. The unforeseen links between Pascal’s triangle, counting methods and the coefficients of polynomials. Is there an underlying truth that can be found linking these?
- Int: The properties of Pascal’s triangle were known in a number of different cultures long before Pascal (eg the Chinese mathematician Yang Hui).
-
How many different tickets are possible in a lottery? What does this tell us about the ethics of selling lottery tickets to those who do not understand the implications of these large numbers?
|
| 1.4 |
Proof by mathematical induction. |
Links to a wide variety of topics, for example, complex numbers, differentiation, sums of series and divisibility. |
- TOK: Nature of mathematics and science. What are the different meanings of induction in mathematics and science?
- TOK: Knowledge claims in mathematics. Do proofs provide us with completely certain knowledge?
- TOK: Knowledge communities. Who judges the validity of a proof?
|
| 1.5 |
- Complex numbers: the number
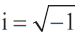 ; the terms real part, imaginary part, conjugate, modulus and argument. ; the terms real part, imaginary part, conjugate, modulus and argument.
- Cartesian form z = a + ib .
- Sums, products and quotients of complex numbers.
|
When solving problems, students may need to use technology. |
- Appl: Concepts in electrical engineering. Impedance as a combination of resistance and reactance; also apparent power as a combination of real and reactive powers. These combinations take the form z = a + ib .
- TOK: Mathematics and the knower. Do the words imaginary and complex make the concepts more difficult than if they had different names?
- TOK: The nature of mathematics. Has “i” been invented or was it discovered?
- TOK: Mathematics and the world. Why does “i” appear in so many fundamental laws of physics?
|
| 1.6 |
Modulus–argument (polar) form The complex plane.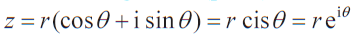 |
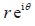 is also known as Euler’s form. is also known as Euler’s form.- The ability to convert between forms is expected
- The complex plane is also known as the Argand diagram.
|
- Appl: Concepts in electrical engineering. Phase angle/shift, power factor and apparent power as a complex quantity in polar form.
- TOK: The nature of mathematics. Was the complex plane already there before it was used to represent complex numbers geometrically?
- TOK: Mathematics and the knower. Why might it be said that eiπ + 1 = 0 is beautiful?
|
| 1.7 |
- Powers of complex numbers: de Moivre’s theorem.
- nth roots of a complex number.
|
Proof by mathematical induction for n ∈ Z+ . |
- TOK: Reason and mathematics. What is mathematical reasoning and what role does proof play in this form of reasoning? Are there examples of proof that are not mathematical?
|
| 1.8 |
- Conjugate roots of polynomial equations with real coefficients.
|
|
|
| 1.9 |
- Solutions of systems of linear equations (a maximum of three equations in three unknowns), including cases where there is a unique solution, an infinity of solutions or no solution
|
- These systems should be solved using both algebraic and technological methods, eg row reduction.
- Systems that have solution(s) may be referred to as consistent.
- When a system has an infinity of solutions, a general solution may be required.
- Link to vectors in 4.7.
|
- TOK: Mathematics, sense, perception and reason. If we can find solutions in higher dimensions, can we reason that these spaces exist beyond our sense perception?
|
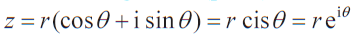


 using both the formula and technology is expected. Link to 5.4.
using both the formula and technology is expected. Link to 5.4.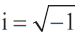 ; the terms real part, imaginary part, conjugate, modulus and argument.
; the terms real part, imaginary part, conjugate, modulus and argument.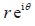 is also known as Euler’s form.
is also known as Euler’s form.