Solution 1: At the North Pole
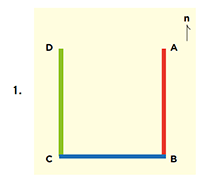 Normally if you follow the path described, you would expect to end up 1 km west of your starting point.
Normally if you follow the path described, you would expect to end up 1 km west of your starting point.
Start at A and walk 1 km south along the red line to B. Then turn west and walk 1 km along the blue line to C. Then turn north and walk 1 km along the green line to D. It would seem that D is 1 km west of A, but this is not quite true, because the Earth’s surface is not flat and AB and DC are not parallel lines on a plane surface. When you walk north or south, you are following a line of longitude. These lines meet at the North Pole and at the South Pole. Check this on a globe of the Earth.
If you are in the Northern Hemisphere, A and D would be less than 1 km apart; in the Southern Hemisphere they would be more than 1 km apart. The difference becomes extreme as you approach the North and South Poles.
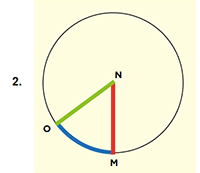 One answer to our puzzle is to start at the North Pole, which we label N. (In this image you are above the North Pole looking down.)
One answer to our puzzle is to start at the North Pole, which we label N. (In this image you are above the North Pole looking down.)
From there, any direction you face is south. Walk 1 km along the red line to M. Now turn west and walk 1 km, which means following a line of latitude 1 km south of the North Pole. All lines of latitude are circles, but this circle is small, so the curvature is much more noticeable than it would be if you were following a line of latitude closer to the Equator.
Now, having arrived at point O, 1 km west of M, you turn north and walk 1 km, bringing you back to your starting point at the North Pole.
Solution 2: Near the South Pole
There’s another solution we know about. In this diagram we are above the area near the South Pole looking down.
Our starting point is J, which is 1 km north of K. The circle is 1 km in circumference, so its radius is 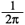 km.
km.
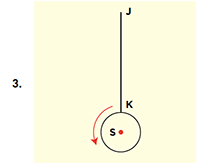 Following the original instructions we face south and walk 1 km from J to K. Then we face west and walk 1 km (in the direction of the red arrow). This brings us back to K. We then face north and walk 1 km, which brings us back to our starting point at J.
Following the original instructions we face south and walk 1 km from J to K. Then we face west and walk 1 km (in the direction of the red arrow). This brings us back to K. We then face north and walk 1 km, which brings us back to our starting point at J.
Any point 1 + 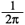 km from the South Pole will do.
km from the South Pole will do.
(Note: If we use  = 3.1416, then J is 1 + 1/2 x 3.1416 = 1.1592 km from the South Pole.)
= 3.1416, then J is 1 + 1/2 x 3.1416 = 1.1592 km from the South Pole.)
Actually, this isn’t quite right. There’s a small detail that we’ve ignored. In calculating the distance from point K on the circle to the South Pole, we’re assuming that the Earth is flat. In reality this distance is along the curved surface of the Earth, which makes it slightly longer than it would be if the Earth were flat.
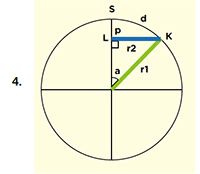 In the diagram here we are looking sideways at a slice through the Earth with the South Pole at the top. The radius of the circle we calculated above as
In the diagram here we are looking sideways at a slice through the Earth with the South Pole at the top. The radius of the circle we calculated above as  km is actually r2, the distance from K, which is on the circle to L, which is a point inside the Earth below the South Pole. The distance d along the surface from K to S is slightly longer. How much longer?
km is actually r2, the distance from K, which is on the circle to L, which is a point inside the Earth below the South Pole. The distance d along the surface from K to S is slightly longer. How much longer?
Here’s how we figure it:
In the diagram
-
- r1 = radius of Earth in km
- r2 =
 km
km
- a = angle in radians between the line from K to the center of the Earth and the line from S to the center of the Earth.
- d = (curved) distance from South Pole to the circle.
- p = distance from S to L
Then
-
- d = r1 x a
- a = asin(r2/r1)
- with r1 = 6378 km
and r2 = 0.15915494309189533576888376337251 km
- a = 2.49537e-5 radians
- d = 6378 km x 2.49537e-5
- = 0.159154943108412676007288479527260 km
So the difference between r2 and d is very small. They are equal up to 9 decimal places. The difference is little more than 10 nanometers!
 In this puzzle we challenge you to figure out where in the world you must be based on the information we give you.
In this puzzle we challenge you to figure out where in the world you must be based on the information we give you.
