Polyominoes

This puzzle asks how many combinations you can make with geometric objects.

Everyone knows what a “domino” is: a game piece made of two adjacent squares. A domino has anywhere from zero to six dots in each square, and most of the games played with dominoes involve matching two dominoes with the same number of dots.

Mathematicians like to generalize. In 1953 a mathematician named Solomon Golomb invented the idea of polyominoes: geometric objects made by connecting a certain number of squares with their sides matching. You can think of polyominoes as solid objects that can be picked up and moved around. There are many puzzles that can be made using polyomino pieces.

Here are a few sample polyominoes:

Monomino

Domino

Tromino

Tetromino

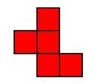
Pentomino

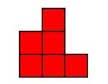
Hexomino

You can form polyominoes with any number of squares. As you can see, there is only one way to form a monomino or a domino; however, there are increasingly more ways to form every other type of polyomino. For instance, there are two ways to form trominoes:

A Little Warm-up Problem

There are exactly five different tetrominoes (shapes made from four squares). Can you find them? Can you prove that there are no more than five? Draw your results on graph paper.

You may want to make or get some square tiles or cubes and actually build your tetrominoes before you draw them on graph paper.

An interesting question

How can you be sure that two tetrominoes are different? For example, here are two tetrominoes that look different, but mathematically they are the same. Can you see why?

Trtromino A B

Tetrominoes A and B are congruent. If you picked up tetromino A and rotated it 90 degrees to the right, you could show that it would fit exactly on top of tetromino B. This is one common test that can be used to determine whether any two 2-dimensional shapes are congruent. Think of tetrominoes as objects that can be picked up and moved around. If you can pick up one of the shapes and rotate it, flip it over, and/or slide it so that it fits exactly on top of the other shapes, then the two shapes are congruent.

The Main Problem

Find all the possible pentominoes: shapes made by linking exactly five squares so that they match along at least one edge. How many different pentominoes can you find? How will you know you’ve found all of them? Draw your results on graph paper.

A big hint

If you take a checkerboard and remove the four corner squares, you’ll have a pattern on which all the different pentominoes will fit exactly. If you can fit all your different pieces onto this shape, you will have found all the possible pentominoes. (This is not an easy task however. It takes trial and error, spatial visualization, and lots of patience.)

An Extra Challenge

After you are sure that you’ve found all the pentominoes, see if you can find all the possible hexominoes, shapes made from six squares. Draw your results on graph paper.

Background

There is a wealth of mathematical problems that can be posed and solved using polyominoes. You’ll find hundreds of them in a book by Solomon W. Golomb titled Polyominoes: Puzzles, Patterns, Problems, and Packings (Princeton University Press, 2d ed., 1994). In it you’ll find literally hundreds of problems, many of which can be tried out for fun as geometric puzzles. If you’re a serious mathematician, you’ll find plenty of proofs, as well as many intriguing conjectures that have not yet been conclusively proven (at least as of the publication of this book).

There are three powerful mathematical ideas that are involved in this month’s puzzles. The first of these is the concept of congruence, introduced above.

Mathematically, two shapes are congruent if they have the same size and shape, regardless of their orientation. If you can pick up one of the shapes and rotate it, flip it over, and/or slide it so that it fits exactly on top of the other shapes, then the two shapes are congruent. This is one simple test for congruence. There are many others.

The second is the idea that you sometimes have to test to be sure whether two mathematical objects are the same or different. Just because two polyominoes look different, you can’t be sure they are different until you’ve picked one up and made sure it’s not congruent to the other. For polyominoes, congruence is the test—but mathematicians have many other tests they can use for different types of problems.

The third is the idea of finding all possible ways to solve a particular problem. This is a common type of problem in combinatorics. For example, find all the possible ways to arrange the numbers from 1 to N. Or for a more everyday example, a restaurant serves pizza with four different toppings: onions, mushrooms, sausages, and extra cheese. How many different types of pizzas can they make using 1, 2, 3, or 4 of the toppings? (Of course, a real restaurant would probably provide many more than four toppings.)

Combinatorics problems involving geometry can be much more complex. For example, if N is the number of squares in a polyomino, there is no known rule or formula that can tell you how many different polyominoes that can be constructed for any value of N. (Mathematicians have worked out the exact number of polyominoes for many values of N, but no general rule has ever been found.)

In addition to Solomon Golomb’s original book, Polyominoes, there have been several other books written about them for serious and recreational mathematicians. If you search the Web for polyominoes, you’ll find thousands of references and even some downloadable polyomino games. If you are familiar with the computer game Tetris, you’ll recognize that the playing pieces are all tetrominoes.

Course:

Math [1]

Result/Solution(s)

Warm-up Problem: Can You Find All Five Tetrominoes?

One strategy for constructing them is to start with both kinds of trominoes and add a square in every possible location. Always check to see if you’ve duplicated one you’ve already made. Here’s how it works:

First start with the straight tromino and add one more square to make a tetromino.

Tromino and tetrominoes

So far you’ve made 3 tetrominoes. Can you make any more from the straight tromino? Think about it. Suppose you put the green square at the top left.

Tetromino

This is congruent to the second tetromino shown above, because if you pick it up and flip it over it will fit exactly on top of the second one. If you put the green square in any other location, it will match one of the first three.

Now start with the corner tromino and see how many you can build. It turns out that you can make four different tetrominoes from the corner tromino.

Tromino and tetrominoes

However, the second and fourth are congruent to two of the ones we made earlier. So there are only two new ones, or five tetrominoes in all.

Tetrominoes

By building tetrominoes systematically in this way, you have also proven that there can’t be any more. You’ve made all the possible combinations of four squares, starting from the two possible trominoes, and eliminated all the duplicates.

The Main Problem: How Many Pentominoes Can You Find?

We can solve this problem using the same method we used for tetrominoes, starting with one tetromino, adding a square in different positions until we’ve found all the possibilities, then going on to the next, until we’ve found them all. Starting with the straight tetromino, we can build three different pentominoes. If you add the green square in any other position, your new shape will be congruent to one of these three.

Pentominoes

You can figure out the rest for yourself, starting with each of the other tetrominoes. It turns out that there are 12 altogether.

Pentominoes

By the way, if you used the hint that all the pentominoes fit on a checkerboard with the corners removed, you could have worked out ahead of time that there had to be exactly 12 pentominoes. A checkerboard has 64 squares. Removing the corners leaves 60 squares. Since each pentomino has 5 squares, there must be 12 all together because 60 / 5 = 12.

Here’s one way they can all fit on the checkerboard:

grid

There are many other pentomino puzzles. We’ll try some of them next month.

You may be interested to know that Solomon Golomb gave all the pentominoes names based on the letters of the alphabet that they resemble. The names are

T, U, V, X, W, Y, Z, F, I, L, P, N

Just for fun, see if you can tell which is which. You may have to rotate or flip the pentominoes to make them look like one of the letters.

An Extra Challenge: How Many Hexominoes Can You Make?

There are exactly 35 different hexominoes! Rather than take the space to show them all here, we’ll let you find them for yourself if you are so inclined. Be sure to check carefully to make sure that you’ve eliminated all duplicates. Good hunting.

combination problems [2]