Our first number series is:
1, 3, 5, 7, 9, 11 . . .
These are odd numbers. They are those that are not evenly divisible by 2. The next three numbers in the series are:
13, 15, 17
For our other number series, the answers are as follows:
a. The series 2, 4, 6, 8, 10, 12 . . . are the even numbers. The even numbers series continues like this:
2, 4, 6, 8, 10, 12, 14, 16, 18 . . .
b. The series 5, 10, 15, 20, 25 . . . are multiples of five. We can keep going:
5, 10, 15, 20, 25, 30, 35, 40 . . .
c. For this series 1, 4, 9, 16, 25 . . . look to square numbers. It may be written like this:
12, 22, 32, 42, 52. . .
and it continues:
12, 22, 32, 42, 52,62, 72, 82. . .
which is the same as:
1, 4, 9, 16, 25, 36, 49, 64 . . .
d. The numbers 1, 2, 6, 24, 120, 720 . . . are factorials. A factorial of a number is the product of all the positive integers from 1 to the given number. The factorial of 3, which is written 3!, is 1 x 2 x 3 = 6. The factorial of 4, is 4! = 1 x 2 x 3 x 4 = 24. Our series of factorials may be written as:
1!, 2!, 3!, 4 !, 5!, 6! . . .
and we may continue it:
1!, 2!, 3!, 4!, 5!, 6!, 7!, 8!, 9! . . .
which equals
1, 2, 6, 24, 120, 720, 5040, 40320, 362880 . . .
Factorials get very big very quickly.
e. In this series 1, 1, 2, 3, 5, 8, 13, 21 . . . the city noted in our hint is Pisa in Italy, which has a famous leaning tower. A man named Leonardo lived in Pisa during the 1200s. His nickname was Fibonacci, and the number series he discovered is named after him. Each number in the series is formed by adding together the two previous numbers.
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5
3 + 5 = 8 . . .
The series continues like this:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 . . .
Fibonacci originally discovered the series by observing and thinking about the growth in a population of rabbits. Click here to find out more about that and other interesting situations in which the Fibonacci series shows up in nature.
|
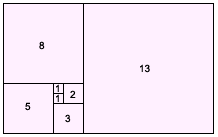
The squares in this pattern follow the Fibonacci sequence. As the pattern continues and the rectangle grows, the ratio of the length to the width of the rectangle gets closer and closer to 1.618034, a number known as the Golden Ratio.
|
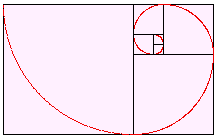
Drawing quarter circles in each of the squares forms a spiral pattern that is similar to that found in some seashells, including the chambered nautilus.
|
f. Our final series 1, 1, 2, 2, 3, 4, 4, 4, 5, 6, 7, 7 . . . was discovered by the mathematician John Conway. It is similar to the Fibonacci series in that each subsequent number in the series is found by adding together two numbers that are already in the series. If that additional hint doesn’t do it for you, click here to find out more.
