All the People in the World

Here's another puzzle that is an example of a Fermi question. This time we ask you to estimate population and land use.

The world population is growing rapidly. At the same time, we are faced with global warming, destruction of rain forests, and other human activities that are reducing the amount of productive land on the planet.

These circumstances generate some intriguing—and vitally important—mathematical/scientific/economic/cultural problems. We pose a few simple ones for this puzzle.

If the entire land area of the Earth were divided equally among all the inhabitants, approximately how much area would each person get?

Figure 1. A map of the world
If the entire productive land on the planet were divided equally among all the inhabitants, approximately how much area would each person get?
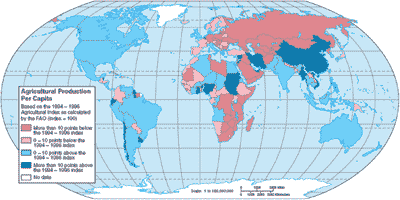^{Source: McGraw-Hill [1]}
Figure 2. Worldwide agricultural land use. The pink regions are places where agricultural production per capita has declined since 1994-96. The blue regions show where per capita production has increased.
How much productive land would be each person’s share in the year 2050 if current population, climate, and economic trends continue?

Figure 3. Visualizing all the people in the world gathered together.
Finally, here’s a little fantasy that’s just fun to think about. If everyone on the Earth were brought together in one place, and given a simple stool to sit on, how much area would it take to hold everyone on Earth? What existing country (or province of a country) would be just about large enough to hold everyone on the planet? How much area would be needed in 2050? What country or region would be large enough to hold everyone at that time?

All the data you’ll need can be readily found on the Internet. You’ll need to make some additional estimates to come up with an answer for part 4.

Background

Fermi questions

This puzzle is the fourth in a series devoted to examples of “Fermi questions ”, named in honor of the Nobel laureate and nuclear physicist Enrico Fermi. Fermi used to give his students problems that involved large numbers, estimates, and approximations. He expected his students to be able to simplify the numbers and do all their calculations on a small piece of paper. They are sometimes called “back of the envelope ” problems. You can find many examples on the Web if you search for “Fermi questions. ”

Fermi questions involve making many assumptions, approximations, and simplifications to try to get a reasonable answer quickly. Your answer doesn ’ t have to be exactly correct — maybe there is no exact answer, because the problem is vague or conditions can vary. A Fermi question does not give you all the information you need; you need to look things up and/or make assumptions.

Global population and land use estimates

There are many sources for information about this, such as national governments, the United Nations, and nongovernmental organizations. You’ll find that there is a reasonable consensus among many sources about expected population growth, while estimates about changes in land mass, land use, and so forth may differ widely among different organizations.

You’ll find all the information at your fingertips if you search the Web for topics such as world population or world land use. Good hunting!

Course:

Math [2]

Result/Solution(s)

Puzzle 1

The first puzzle asks: If the entire land area of the Earth were divided equally among all the inhabitants, approximately how much area would each person get?

To solve this, we’ll need to know the population of the Earth and its total landmass.

Let's assume the population of the Earth is 6,567,264,420 people and the world landmass is estimated at 510,072,000 square km. To find each human’s share of the planet’s land, we divide the land by the population. It’s not so easy to accurately divide 510,072,000 by 6,567,264,420, even with a hand calculator. Fortunately, for a Fermi question we don’t need to be so accurate. We can round off the numbers to get approximate answers. Let’s divide 510,000,000 (5.1 x 10⁸, or 510 million) by 6,570,000,000 (6.57 x 10⁹, or 6.57 billion).

Scientific notation is a good format to use when multiplying and dividing large numbers. If you are not familiar with scientific notation, here’s one of many Web sites with a little tutorial [3].

So, now let’s divide 5.1 x 10⁸ / 6.57 x 10⁹ = .776 x 10^-1 or .776 . . . x 0.1 = 0.0776 sq km/person.

One hectare is equal to 0.01 sq km. We have to multiply sq km by 100 to get the number of hectares. So each person’s share of the total world landmass is about 7.76, or about 7 3/4 hectares. That’s enough for a large garden or a very small farm. But can this land be used for gardening or farming?

8,563,533,380 hectares is productive land, while all the world’s landmass is 510,072,000 sq km. Multiplying the sq km by 100, we get 51,007,200,000 hectares. The percentage of all the world’s land that is productive land is approximately 8.56 x 10⁹ / 5.1 x 10¹⁰ = 0.168 (16.8%, just over one-sixth).

Puzzle 2

In this puzzle we want to find out if the entire productive land on the planet were divided equally among all the inhabitants, approximately how much area would each person get?

Productive land is all the land that can be used for planting crops, (arable land), plus pasture land and forests. This is a much smaller area. The World Clocks Web site estimates that productive land on the planet is currently 8,563,533,380 hectares.

We round off the productive land estimate to 8.56 x 10⁹ hectares and divide the number of people by the world productive land to get

8.56 x 10⁹ / 6.57 x 10⁹, or about 1.30 hectares per person.

Puzzle 3

The question in this puzzle is how much productive land would be each person’s share be in the year 2050 if current population, climate, and economic trends continue?

One source for estimates of world population growth is the US Census Bureau Web site [4]. This links to a list of estimated world population in the middle of each year from 1950 through 2050. The estimate for 2050, just 43 short years from now, is a whopping 9,404,296,384, approximately 9.4 billion!

We need to do a bit more work to estimate the amount of productive land remaining worldwide in 2050. According to the World Clocks Web site, “data on productive land are extrapolated from statistics produced by the United Nations Food and Agriculture Organization . . . one hectare is lost every 7.67 seconds.” We don’t know whether this rate of loss will continue, slow down, or speed up, so let’s assume it stays the same.

1 hectare / 7.67 seconds = 0.130 hectares/second.

Now we need to know how many seconds there are in 43 years. Well, there are 3,600 seconds/hour, 24 hours/day, and 365 days/year. We multiply these together:

3,600 sec/h x 24 hr/day x 365 days/yr x 43 yr = 31,536,000 x 43 =
3.1536 x 10⁷ x 43 = 135.6048 x 10⁷ = 1.36 x 10⁹ seconds.

We multiply this by 0.13 hectares/second:

1.36 x 10⁹ x 1.3 x 10^-1 = 1.77 x 10⁸ hectares lost in 43 years.

Currently (2007) there are about 8.56 x 10⁹ hectares.

8.56 x 10⁹– .177 x 10⁹ = 8.38 x 10⁹ hectares of productive land remaining in 2050.

Now, how much productive land per person in 2050? The population estimate is 9.4 billion. So to find everyone’s share of land:

8.38 x 10⁹ hectares / 9.4 x 10⁹ persons = 0.89 hectares/person.
down from 1.30 hectares/person using our initial population estimate.

That’s a drop of (1.30 - .89) / 1.30 = .41 / 1.30 = 31.5% less than in our initial population estimate.

This would make for a very hungry, possibly angry world! It’s clear—we the people of the world have to do something to change the way things are going, so this doesn’t happen.

Puzzle 4

Puzzle 4 asks: If everyone on the Earth were brought together in one place and given a simple stool to sit on, how much area would it take to hold everyone on Earth? What existing country (or province of a country) would be just about large enough to hold everyone on the planet? How much area would be needed in 2150? What country or region will be large enough to hold everyone at that time?

Here we need to use our creative thinking a bit. Of course there is no practical way to bring everyone in the world together. The logistics of getting everyone to one place, not to mention feeding and housing them, would make another complicated Fermi question and probably could never happen.

However as a fantasy, suppose we have all 6.57 billion people together, in one area. How much space would that many people take up? Well, it depends on how much space we allow per person. Let’s start from a minimal amount of space. Suppose we allow everyone 1 sq m for their stools and themselves. This will make the calculation relatively simple. We’d need 6.57 billion square meters. That’s 6.57 x 10⁹ sq m. How many sq km is that. A sq km is a square 1,000 m on a side. So 1 sq m = 1,000,000 = 10⁶ sq km.

6.57 x 10⁹ / 1 x 10⁶ = 6.57 x 10³ sq km, 6,570 sq km.

Hmmm. That’s not so big. Everyone in the world could fit on the island of Puerto Rico, a commonwealth that’s part of the United States and contains 9,104 sq km (3,515 sq mi) of land.

If we want to be a little more practical and allow some additional spaces between people, so there can be streets for them to walk on, ways to transport food and medical supplies, and so forth, perhaps we need to allow an average of 3 m/person (10 ft/person). This means we’d need three times as much as 6,570 sq km which works out to 19,710 sq km (7,610 sq mi) The countries of Slovenia (20,273 sq km; 7,827 sq mi), Israel (20,770 sq km; 8,019 sq mi) and El Salvador (21,070 sq km; 8,135 sq mi) are the smallest that could accommodate all the people in the world.

As we project ahead to the year 2050, when there may be about 9.4 billion people, if we estimate an average of 3 sq m per person, we’d need an area of 28.2 x 10³, or 28,200 sq km (10,888 sq mi). The Solomon Islands, with an area of 28,450 sq km (10,985 sq mi) is the smallest country that can accommodate that many people. However, since the Solomon Islands are spread out over many kilometers of the Pacific Ocean, we would not be able to bring everyone in the world together. Albania, with an area of 28,748 sq km (11,100 sq mi) is therefore the smallest country that could hold all the world’s people in one place.

Math Puzzle [5]