Hours, Minutes, and Seconds

The three scales on a clock—hours, minutes, and seconds—form the basis for many different puzzles. This puzzle asks if the scales align more than twice each day.

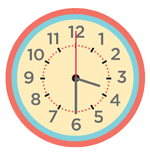Clock A clock is a complicated measuring device. There are three scales superimposed on each other, one for hours, one for minutes, and one for seconds.

On the clock shown here, the hours are numbered and there are marks for each minute. We all know that the minute hand on the 6 represents 30 minutes, not 6 minutes past the hour. Since the hour hand is between 3 and 4 and the second hand is at 12, we know that the time is 3:30:00.

In this puzzle we introduce an idea of the “minute position” of the hour hand. At 3:30:00, the minute position of the hour hand is 17 1/2 minutes. The hour hand is pointing at the 17 1/2-minute mark on the clock face, because that is the minute position exactly halfway between the hours of 3 and 4.

Clock At 3:30:00, and any time that the minute hand points exactly to one of the minute marks, the second hand points to the 12. By the time the second hand has moved another 30 seconds, so that the time is 3:30:30, the minute hand will have moved halfway to the next minute mark, as shown below. (The hour hand will have moved a tiny bit as well.)

Another important convention about clocks and time is that the minute, hour, and second hands start counting at zero, every time they sweep through a full revolution on the clock. Every 12 hours the hour hand starts over at 0. Also, every 60 minutes, the hour hand moves five “minute places” further along and the minute hand starts over at 0. Similarly every 60 seconds the minute hand moves one minute place further along and the second hand starts over again at 0.

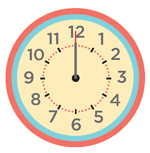Clock When the hour, minute, and second hands point to 12, the time is 12:00:00, which could also be called 00:00:00.

Now here’s your puzzle.

The hour, minute, and second hands are exactly aligned with one another at 12:00. There may be some other times when all three hands are close to one another; however, is there any time other than 12:00 that all three hands line up exactly?

On some clocks the second hand moves in “ticks,” pausing briefly at each mark on the clock face. For this puzzle, assume that the hour, minute, and second hands of the clock move continuously.

Hints:

To solve this problem, it would be best to answer the following questions first:

How many times in a 12-hour cycle for the hour hand are the hour and minute hands exactly aligned with each other? Can you determine the specific times those occur in hours, minutes, and seconds?
How many times in a 1-hour cycle are the minute and second hands exactly aligned with each other? Can you determine the specific times those occur in minutes and seconds?

Background

The mathematics of time is complicated partly because of the cyclical nature of time measurement. Cyclical arithmetic, also called modular arithmetic and sometimes called “clock arithmetic”, is an important branch of mathematics and has many applications in science. Our normal numbering starts at zero and continues on forever with larger and larger positive and negative numbers. Cyclical or modular numbers also start at zero and begin to increase until a certain value is reached, at which point they start again at zero. Arithmetic problems in such systems have a beauty and difficulty all their own.

The mathematics of time is also complicated because we use so many different, although related units. Arithmetic problems involving time can be extremely complex. Think about it: 60 seconds per minute, 60 minutes per hour, 24 hours per day, 365 days per year. Not to mention weeks and months! (The convention for hours, minutes, and seconds goes back to the ancient Babylonian convention of dividing a circle into 360 degrees.)

The system defies logic! Indeed, at the time of the French Revolution, French scientists proposed that the world adopt a new system for time measurement based on decimal arithmetic. After all, their metric system had become standard throughout the world. Why not have a metric system for time? In the French Revolutionary system the year had ten months, thirty days each; each month had three ten-day weeks; each day ten hours; each hour 100 minutes; each minute 100 seconds. The French system is described in Wikipedia [1].

Metric time never caught on for many reasons. For one thing, all the clocks and watches already in existence would have become obsolete!

Course:

Math [2]

Result/Solution(s)

Solution: Hours, Minutes, and Seconds Math Puzzle

First let’s find out how many times the minute hand and hour hand exactly match over a 12-hour cycle. The hands start together at 12:00

Between 12:00 and 1:00, the minute hand is always ahead of the hour hand. Then somewhere slightly past 5 minutes after 1:00, the hour and minute hands are in the exact same position. If you have a clock or watch on which you can manipulate the time, try this for yourself.

In this way, the minute hand will pass over the hour hand ten more times, once each hour between 1 and 2, 3 and 4, and so on, until the hour between 10 and 11. Between 11 and 12, the minute hand never catches up to the hour hand until exactly 12:00, when the hands line up again. The hands match up 12 times in a complete cycle, including both the starting and ending positions.

Next we think about how often the second hand and minute hand match each other exactly. The pattern is the same, but the number of occurrences is different. The hands match exactly at 00:00. Between 00:00 and 01:00 the second hand is always ahead of the minute hand; between 01:00 and 02:00, the hands cross exactly once, and do so again for every minute until 59:00 to 60:00, when the second hand does not catch the minute hand until exactly 60:00. The hands match up exactly 60 times an hour, including both the starting and ending positions.

You might conjecture that since the hour and minute hands match 12 times and the minute and hour hands match once each minute, there is a good chance that all three will match at some point during the hour. However, in order to test that conjecture we need to do some exact calculations. Start with the hour hand and minute hand. Every time the minute hand moves 60 minutes, the hour hand moves 5 minutes along the clock dial. Or, every time the minute hand moves 12 minutes the hour hand moves 1 minute.

If MP is the minute position of the hour hand, H is the hour, and M is the number of minutes past the hour, then

MP = 5H + M / 12

To find out exactly when the minute and hour hand overlap, we set the minute position of the hour hand equal to the number of minutes, to see if there’s a solution;

M = 5H + M / 12.

Multiplying both sides by 12, we get

12M = 60H + M

Rearranging, we get

11M = 60H, or M = 60H / 11.

For example when H = 1, M = 60 / 11 = 5 - 5 / 11 minutes. In other words, the hour and minute hand will match at exactly 01:05 - 5 / 11. Converting 5 / 11 minutes to seconds, we multiply by 5 / 11 by 60 to get 27 - 3 / 11 seconds, for a precise time of 01:05:27 - 3 / 11. Substituting H = 2, 3, 4, and so forth, in equation (3) we can make a table of results.

Hour (H)	Minutes Past the Hour (M)	Exact Time in Hours, Minutes, and Seconds
12-1	0	12:00:00
1-2	5 - 5 / 11	01:05:27 - 3 / 11
2-3	10 - 10 / 11	02:10:54 - 6 / 11
3-4	16 - 4 / 11	03:16:21 - 9 / 11
4-5	21 - 9 / 11	04:21:49 - 1 / 11
5-6	27 - 3 / 11	05:27:16 - 4 / 11
6-7	32 - 8 / 11	06:32:43 - 7 / 11
7-8	38 - 2 / 11	07:38:10 - 10 / 11
8-9	43 - 7 / 11	08:43:38 - 2 / 11
9-10	49 - 1 / 11	09:49:05 - 5 / 11
10-11	54 - 6 / 11	10:54:32 - 8 / 11
11-12	60	12:00:00

Now let's do a similar calculation to find out exactly when the minute and second hands match each other.

At the beginning of each minute, the second hand is on 0. Every time the second hand moves 1 second, the minute hand moves 1 / 60 of a minute around the clock.

Between minute M and minute M + 1, the position of the minute hand is given by

M + S / 60.

To see when the second hand is exactly equal to the minute hand, we set this equal to the number of seconds, S.

S = M + S / 60 (5).

Multiplying both sides by 60, then regrouping and solving for S in terms of M, we get

S = 60M / 59.

This tells us that every minute, there will be a place, expressed in a number of seconds and 59ths of a second, where the two match exactly.

Now we can give the answer to our puzzle. The conjecture that all three hands match at times other than 12:00:00 is false. All three hands can never meet except at 12:00:00. This is because the times for second hand–minute hand matching are all given in 59ths of a second, and the times for minute hand–hour hand matching are all given in 11ths of a second. Since 11 and 59 are both prime numbers, there is no way the two fractional values can be exactly equal, no matter how close they come.

If we want to complete the calculation, we can see exactly where the second and minute hands match during each of the minutes for which the hour and minute hands match. This involves a lot of calculations, but it will show how close the times come to matching.

Hour (H)	Minutes Past the Hour (M)	Hour and Minute Hand Matching Times M = 60H / 11	Minute and Second Hand Matching Times S = 60M / 59
12 - 1	0	12:00:00	12:00:00
1 - 2	5 - 6	01:05:27 - 3 / 11	01:05:05 - 5 / 59
2 - 3	10 - 11	02:10:54 - 6 / 11	02:10:10 - 10 / 59
3 - 4	16 - 17	03:16:21 - 9 / 11	03:16:16 - 16 / 59
4 - 5	21 - 22	04:21:49 - 1 / 11	04:21:21 - 21 / 59
5 - 6	27 - 28	05:27:16 - 4 / 11	05:27:27 - 27 / 59
6 - 7	32 - 33	06:32:46 - 7 / 11	06:32:32 - 32 / 59
7- 8	38 - 39	07:38:10 - 10 / 11	07:38:38 - 28 / 59
8 - 9	43 - 44	08:43:38 - 2 / 11	08:43:43 - 43 / 59
9 - 10	49 - 50	09:49:05 - 5 / 11	09:49:49 - 49 / 59
10 - 11	54 - 55	10:54:32 - 8 / 11	10:54:54 - 54 / 59
11 - 12	60	12:00:00	12:00:00

The three hands come closest to matching between 3:16 and 3:17, when the minute and second hands match about 5 seconds before the minute and hour hands, and also between 8:43 and 8:44, when the minute and second hands match about 5 seconds after the minute and hour hands.