This problem is simple if you consider the symmetry of the cube blocks. A cube can be rotated in different directions. If any two blocks can be rotated so that both look identical, then they should be considered “the same.”
If, for example, blocks A and B both have two adjacent faces painted blue and four other faces painted red, then one can be rotated to look just like the other.
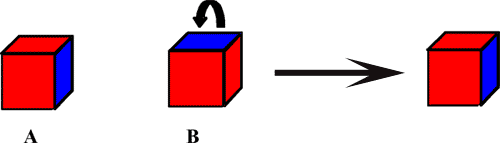
When block B is rotated so that the red face at the right is on top, it looks just like block A.
There is another kind of symmetry that can help solve this problem. If there is one pattern with two adjacent faces blue and four faces red, there is a corresponding, different pattern with two adjacent faces red and all the rest blue.
A table will help keep track of all the possibilities.
|
all red
|
all blue
|
|
5 faces red, 1 blue
|
5 faces blue, 1 red
|
|
2 opposite faces blue, 4 other faces red
|
2 opposite faces red, 4 other faces blue
|
|
2 adjoining faces blue, 4 other faces red
|
2 adjoining faces red, 4 other faces blue
|
|
3 faces in one corner red, opposite corner blue
|
Same
|
|
3 sequential faces red, 3 other sequential faces blue
|
Same
|
These add up to ten different ways to paint the cubes. When all the blocks in the set are painted, there will be ten distinct patterns on the cubes.


