Chapter 13: General division (Paravartya)

The study of division is divided into two parts:

Part A: When the divisor is less than the base
Part B: When the divisor is more than the base

Part A

The format of division is presented in the diagram below:

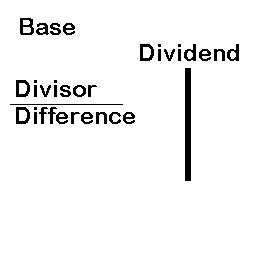
We will divide the dividend in two parts. The RHS will contain as many digits as the number of zeros in the base. The final answer obtained on the LHS is the quotient and RHS is the remainder.

Divide 23 by 9.

The devisor is 9, the base is 10 and the difference is 1 (10 – 9 = 1)

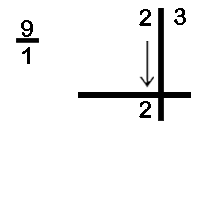
Next since the base 10 has one zero in it we divide the dividend in such a way that the RHS has one digit.

We now bring down the first digit of the dividend that is 2 as per the diagram below.

Next, we multiply 2 with the difference 1 and add the answer to the next digit of the dividend as shown below:

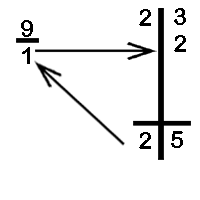
The product of 2 and 1 (the difference ) is 2 which written below 3 and then we add 2 & 3 to get the remainder as 5

Thus when 23 is divided by 2 the quotient is 2 and the remainder is 5

Divide 31 by 9

The divisor is 9, the base is 10 and the difference is 1. We divide the dividend in two parts with one digit on the RHS as there is one zero in the base.

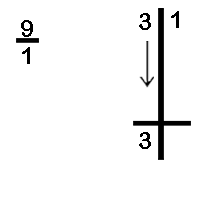
We write down the first digit of the dividend 3 as shown above

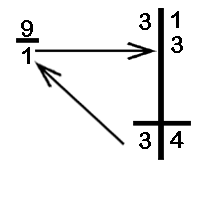
Next we multiply the 3 written down with the difference 1. The product so obtained is written below the second digit of the dividend.

Finally, we add the digits 1 and 3 to get the answer 4.

Thus, the quotient is 3 and the remainder is 4.

Examples:

(A) (B)

Divide 44 by 9 Divide 71 by 9

10 10

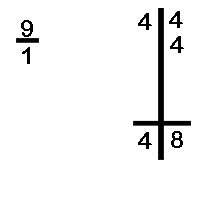
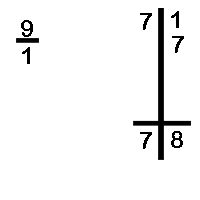
In example (A) we bring down the first digit from the dividend, viz. 4. Next, we multiply the 4 with the difference 1 and write it below the second digit of the dividend. The total of the RHS is 8. Thus the quotient is 4 and remainder is 8.

In example (B) we bring down the first digit of the dividend. viz. 7. Next, we multiply the 7 with the difference 1 and write the answer below the second digit of the dividend. The total of RHS is 1 plus 7 equal to 8. Thus, the quotient is 7 and the difference is 8.

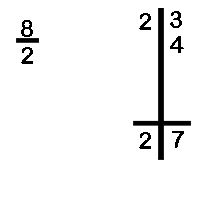
Divide 31 by 8

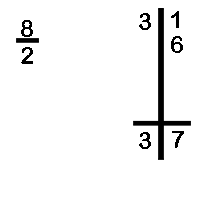
In this case the dividend is 31 and the divisor is 8. We divide 31 into two parts with the right hand side having as many digits as the number of zeros in the base. Since, the base ten has one zero we have one digit in the RHS of dividend.

We write the divisor as 8 and the difference below it as 2

We bring down the first digit of the dividend 3 as it is

We multiply the 3 with the difference 2 and get the product 6. This is written down below the second digit of the dividend, viz. 1. The total is 7. Hence, the quotient is 3 and the remainder is 7.

More Examples:

(A)

(B)

Divide 24 by 8

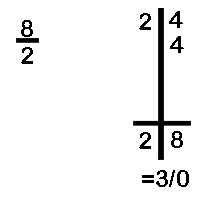
Note Here that remainder is 8 which is equal to the divisor, but the remainder should always be less than the divisor, so we further divide the remainder 8 by divisor 8 to get the final remainder as 0 and add 1 to the quotient (2+1=3 is the final quotient)

(C)

Divide 42 by 8

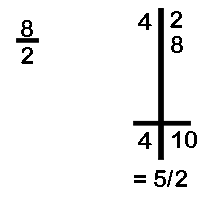
In example (A) we bring down the first digit 2. Next, we multiply 2 with the difference, viz, 2. The total is 4 and is written below the second digit of the dividend. The quotient is 2 and the reminder is 7.

In example (B) we bring down the first digit 2. Next, we multiply 2 with 2 and get the answer 4. The total of RHS is 8 in this case, we have the quotient as 2 and the remainder is 8 but the remainder 8 so obtained it self equal to the divisor hence, we increase the quotient by one unit and take the remainder as zero. The final quotient is 3 and the final remainder is 0.

In example (C) the quotient is 4 and the remainders is 10.the number 10 can be further divided by 8 to get a quotient 1 and remainder 2. We increases the quotient by 1 and take the remainder 2. thus, when 42 is divided by 8 the quotient is 5 and remainder is 2.

Divisors

100

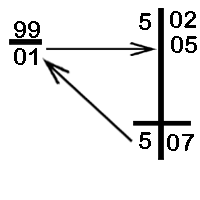
The quotient is 5 and the remainder is 7

Divide 617 by 95

100

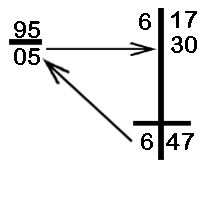
In this case we write down the first digit of the dividend as it is. We multiply 6 with the difference 5 and write the answer 30 below the RHS. The total of RHS is 47. Thus, the quotient is 6 and the difference is 47.

In all the examples that we have seen above, we split the dividend into LHS and RHS. However, there was only one digit in the LHS. We will now take a look at how to solve example where the dividend is big and the LHS has more than one digit.

Divide 123 by 9

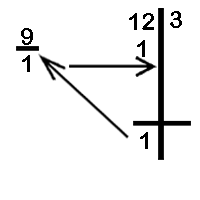
The base 10 has one zero and therefore we split the dividend in such a way that the RHS has one digit
Now we are left with two digits on the LHS.
We bring down the first digit 1 as it is.
We multiply the 1 with the difference 1 and put the answer below the second digit of the dividend.
The second digit of the dividend is 2 and we add 1 to it the total is 3

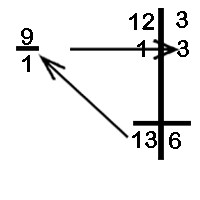
We now multiply the total 3 with the difference 1 and write the product, viz. 3 below the third of the dividend
The total is 6
Thus, the quotient is 13 and the remainder is 6.

Divide 1234 by 98

100

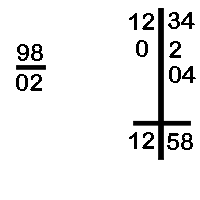
We bring down 1 and multiply it with 02. The product 02 is written down from the second digit of the dividend.
We now add 2 plus 0 downwards and get the second digit of the quotient. The answer is 2
We multiply 2 with 02 and the final answer 04 is written down from the third digit of the dividend
We add up the numbers on the RHS from the extreme digit column. The total of 4 + 4 is 8. We come to the column the left and add 3 + 2 + 0 = 5
Hence, the product is 12 and the remainder is 58.

(In the above example, the difference of 100 and 98 is taken is 02. If we take the difference as 2 instead of 02 we will get incorrect answer.)

Divide 2122 by 97

100

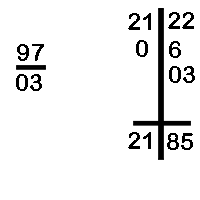
We bring down the first digit of the dividend - 2.
2 multiplied by the difference 03 gives 06 which is written just below the second digit of the dividend.
We now add 1 plus 0 downwards and get the second digit of the quotient as 1.
We now multiply 1 with 03 and get the answer 03, which is written below the third digit of the dividend.
The quotient is 21 and the remainder (obtained by adding up the values in RHS) is 85

Divide 12311111 by 99970

100000

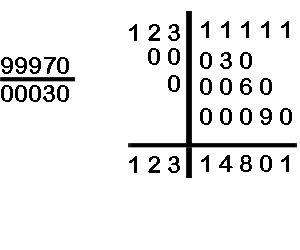
In this case we have a three digit quotient. The number 1,2 and 3 are successively multiplied with 00030 to get th final answer. The quotient is 123 and the remainder is 14801

MISCELLANEOUS EXAMPLE

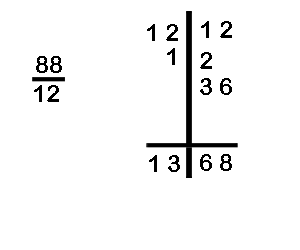
(a) Divide 1212 by 88

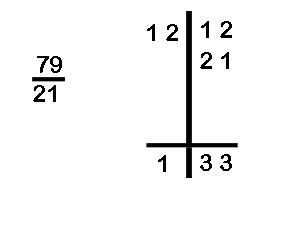
(b) Divide 112 by 79

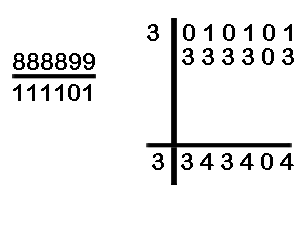
(c) Divide 3010101 by 888899

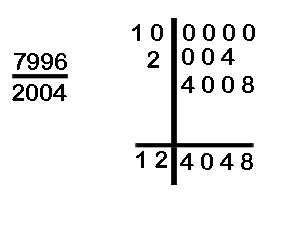
(d) Divide 100000 by 7996

(e) Divide 30001 divided by 88

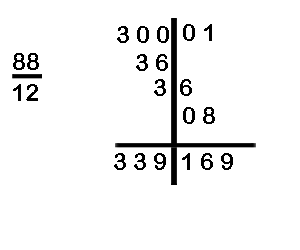
= 340/81

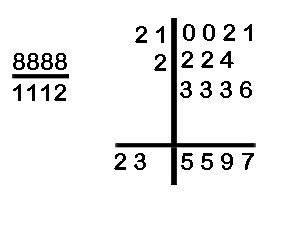
(f) Divide 210021 by 8888

(g) Divided 20407 by 8987

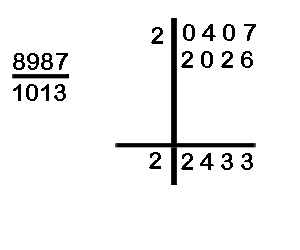
(h) Divide 11007 by 799

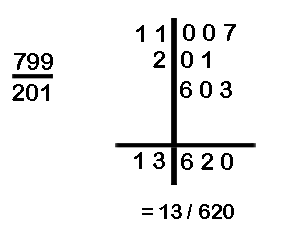
(In example (g) and (h) there is a carry-over involved on the RHS.)

(i) Divide 2211 by 88

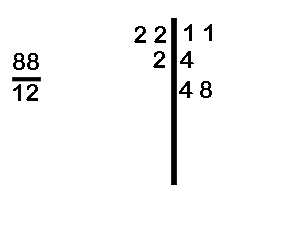
(j) Divide 111301 by 897

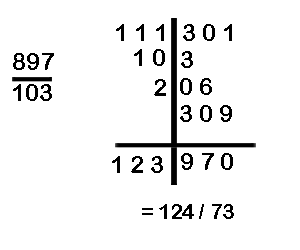
(k) Divide 30122 by 87

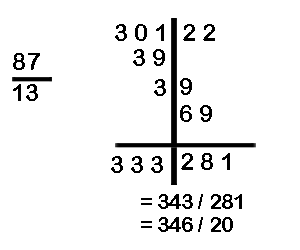
In example (i) the divisor is 88 and the remainder is 99 However, we cannot have the remainder greater than the divisor. Therefore, we increases the value of the quotient by 1 and take the difference as the new remainder (99-88)

In example (j) the divisor is 897 and the remainder is 970.The remainder is greater than the divisor. We increase the value of the quotient by 1 and take the difference as the new remainder (970-897).

In example (k) the total of the third quotient digit is 13. We therefore carry over the 1 to the second quotient digit. The final answer is 343. Next, we will divide the remainder by the divisor and get the new quotient as 346 and new remainder as 20.

EXERCISE

Part A

(a) Divide 102 by 74

(b) Divide 10113 by 898

(d) Divide 1005 by 99

Part B

When the divisor is more than the base

The format and working of this system is the name as explained in th previous part. However, in this case we will have a negative difference.

100

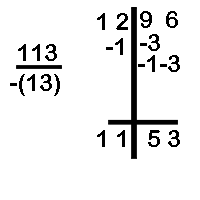
The divisor is related to the base 100 and therefore split the dividend in such a way that the RHS has to digits
The base is 100 and the difference is -13(negative).
We write down the first digit 1 of the dividend as it is.
We multiply 1 with the difference -13 and write answer as -1 and -3 below the second and third digits the dividend.
Next, we go to the second column of the dividend bring down 2 minus 1 is 1.
We multiply 1 with -13 and write -13 and write the answer as -1 and below the last two digit of the dividend
Thus, the quotient is 11 and the difference is 53

(Note in this case we have represented the difference as -1 Alternatively, it can be shown as -1 -3. From the second example onwards we will use the latter way.)

(b) Divide 2688 by 120

100

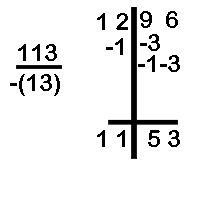
The divisor is 120. Therefore, the base is 100 and the difference is -2-0.

We bring down 2 from the dividend.

we multiply 2 with -2-0 and write the answer as -4-0

Next, we go to the second digit of the dividend

We bring down 6 - 4 = 2.

We multiply 2 with -2-0 and get the answer as 10

Divide 13968 by 1023

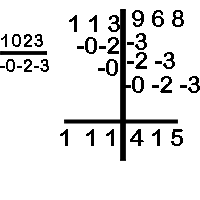
Quotient = 111; Remainder = 415

Divide 1999 by 180

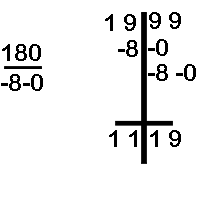
Quotient = 11 Remainder = 19

as we can see that the process used in this system of is ... very much similar to the process that we observed in pervious chapter. Let us now have a look at a variety of ............ and the technique employed in each case............... have a negative answer in the quotient

Divide 14189 by 102

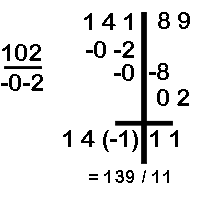
In this case we bring down the first digit 1. We multiply 1 with -0 -2 and write the answer below the second digit as -0-2.
Next we bring down 4-0=4. We multiply 4 by -0-2 and write the answer as -0-8.
Next we bring down 1 -2 -0 = -1 and multiply it with -0 -2 and gate the answer as 0 2. (since both the quotient and divisor are negative the answer will be positive
The quotient is 140 minus 1 equals 139 The remainder is 11.

(f) Divide 110999 by 1321

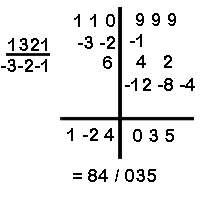
Here the quotient is 100 - 20 + 4 equals 84. The remainder is 035

At times we might have a negative answer in the remainder

(g) Divide 1693 by 131

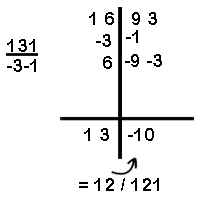
Vedic Math by faculty member Amitesh Amar

Course:

Vedic Math

Or log in with...

Chapter