Chapter

Square root of perfect squares.  This chapter illustrates how to calculate the square root of a perfect square.  For example, 14² = 196 so 

Table of basic squares 1 to 10 must me memorized:

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25

6² = 36

7² = 49

8² = 64

9² = 81

10² = 100

From this table we can determine the calculation between unit digit of a square and its square root.

Unit Digits Of

Square      Square root

Now it can be seen clearly that except for 5 and 0 the relationship between the unit digits of square and square root is not unique, so we get 2 possible unit digits for each unit digit of a perfect square

Note : A perfect square CAN NOT end in 2, 3, 7 or 8 as these digits are not appearing as unit digits of a perfect square

Example :- Now if we want to calculate square root of 4096

Step 1: Write the unit digits as 4 or 6

Step 2: Remove 2 digits from the right of the no.

Step 3: Now refer the remaining no. (40) to the basic square table, 40 lies between 6² and 7²  (6² < 40 < 7²⁾

Step 4: Select smaller square (6) for the ten’s digit of square root

 Now we still have two possible answers

   64 or 66

So how do we resolve this issue? We need to take the assistance of the middle number 65 which lies between 64 and 66

65²  = (6 x 7) / 5²  

       = 4225 (By Ekadhikena-purvena.)

Now by comparing 4096 with 4225

4096 < 4225

Since 4096 is less than 4225 its square root should also be the square root of 4225 (which is 65)

Hence   64 < 65

So the final answer is 64 and not 66.

Example 2

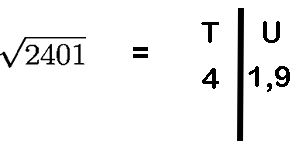
Unit digit 1 or 9 (corresponding to 1)

Ten’s digit is 4 as 4²  <  24  <  5²

So possible answers are 41 or 49

Square of middle no 45² = 2025

As 2401 > 2025

so 

49  >  45

So final answer is 49 and not 41

Example 3:

Example 4:

Example 5:

Example 6:

Exercises:

Now if the square consists of a 5 digit or a 6 digit number then its square root will have 3 digits

Example:

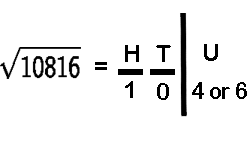
Step 1: Unit digit will be either 4 or 6

Step 2: Remove 2 digits from the right side of the number.

Step 3: 10² < 108 <  11²

So now we have two possible answers 104 or 106

Take the middle no: 105

Compare

Select 104 as final answer

Exercises: