PrintThis chapter has two methods for squaring.
- Method 1: Squaring by the base method
- Method 2: Squaring by using the general formula
Before learning these methods the basic squares of numbers 1 to 10 must be memorized by the students. For your convenience we are providing them:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
Method 1: Squaring by the base method
Example 1: 122 = (12 + 2)/22 = 14/4 = 144
Step 1: Select the closest base 10
Step 2: Calculate the difference 12 – 10 = +2
Step 3: In the LHS add +2 to 12 (i.e 12+2=14)
STEP 4: In the RHS write the square of the difference (22 = 4)
Step 5: Combine the LHS and RHS to obtain the final answer as 144
Note: The rule of carry over states that the number of digits in RHS must be equal to the number of zeros in the base. This rule must be followed here.
Example 2: 142 = (14 +4)/42
= 18/16
= (18 + 1)/6
= 196 (Note that 1 is carried over)
Example 3: 1042 = (104 +4)/42
= 108/16
= 10816
Example 4: 1022 = (102 + 2)/22
= 104/04
= 10404
Example 5: 10122 = (1012 + 12)/122
= 1024/144
= 1024144
Example 6: 942 = (94 – 6)/(-6)2
= 88/36
= 8836 (note here the difference was negative because 94 is lower than the base 100.)
Example 7: 9872 = (987-13)/(-13)2
= 974/169
= 974169
Example 8: 842 = (84 -16)/(-16)2
= 68/256
= 7056 (Note here that 2 is carried over to LHS)
Example 9: 9912 = (991 - 9)/(-9)2
= 982/081
= 982081
Example 10: 882 = (88 - 12)/(-12)2
= 76/144
= 7744 (Note that 1 is carried over)
We can conclude that in the LHS the number has to be increased or decreased by the respective difference from the base. In RHS we have to set up the square of the difference.
Exercises:
132 = 169
162 = 256
1062 = 11236
1092 = 11881
1132 = 12769
10022 = 1004004
10082 = 1016064
10112 = 1022121
10212 = 1042441
10242 = 1048576
912 = 8281
972 = 9409
982 = 9604
9922 = 984064
9892 = 978121
97.62 = 9525.76
98.72 = 9741.69
99.42 = 9880.36
98.12 = 9623.61
99.882 = 9976.0144
Method 2: Squaring by using the general formulae.
The general formula for square of any two digit number ab (here a is the 10th digit and b is the unit digit.)
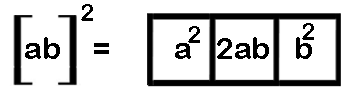
Example 1
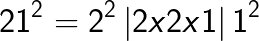
= 441
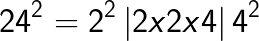
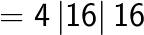
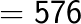(note the carry over)
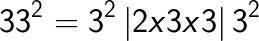
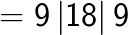
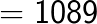
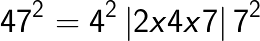
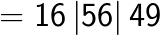
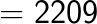
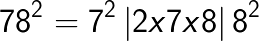
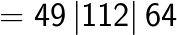
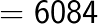(Note that 6 is carried over from the right box to the middle box and 11 is carried over from the middle box to the left box).
Exercises:
222 = 484
232 = 529
362 = 1296
412 = 1681
542 = 2916
632 = 3969
772 = 5929
842 = 7056
882 = 7744
912 = 8281
932 = 8649
9.42 = 88.36 (Note the placing of the decimal after two digits from the right).
962 = 9216
972 = 9409
992 = 9801
Method 2: General formula for squaring of any 3 digit number [abc]. Here a is the 100th digit, b is the 10th digit and c is the unit digit.
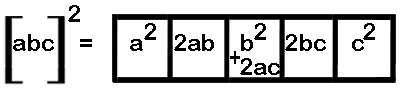
Examples
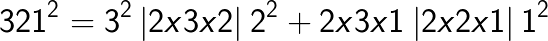
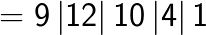
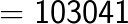
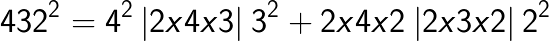
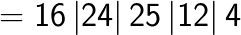
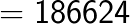
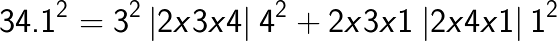
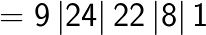
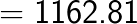(Note the placing of the decimal after two digits from the right in the answer as the question contained the decimal after one digit from the right. You simply double it).
Exercises:
3122 = 97344
4312 = 185761
3242 = 104976
4222 = 178084
7862 = 617796
3522 = 123904
4542 = 206116
2.512 = 6.3001
5.222 = 27.2484
0.5332 = 0.284089
2222 = 49284
7772 = 603729
Course:
