Urdhav means vertically and Tiryak means crosswise. So, this method literally means vertical and crosswise multiplication.
To understand this we will use a simple example:
32 x 21
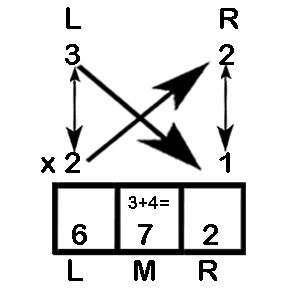
Step 1: Make (2n – 1) boxes where n is equal to the number of digits of the numbers to be multiplied. So, here we will make three boxes since n = 2.
Step 2: Multiply L x L digits vertically and write the product in the left box (3 x 2 = 6)
Step 3: Now multiply L and R digits crosswise (L x R + R x L) and write the sum in the middle box [(3 x 1) + (2 x 2) = 7]
Step 4: Multiply R x R digits vertically and write the product in the right box (2 x 1 = 2)
Step 5: Now derive the final answer from right to left as 672
Example 2: 63 x 23
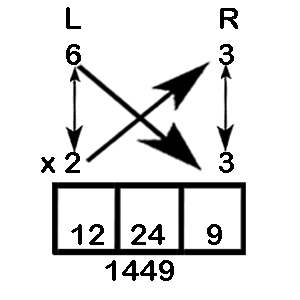
Step 1: 6 x 2 = 12
Step 2: 6 x 3 + 3 x 2 = 24
Step 3: 3 x 3 = 9
Step 4: So we get 12/24/9
Step 5: We now have to perform the carry over to derive the final answer as 1449
Note that we have carried over the digit 2 from the middle box to the left box (12 + 2 = 14)
Example 3: 98 x 87

Step 1: 72 / 63+64 / 56
Step 2: 72/127/56
Step 3: Now perform the carry over to derive the final answer as 8526
Note that we have carried over two digits from middle box to the left box as we can only keep unit digit in each box except the left box.
Example 4: 89 x 7
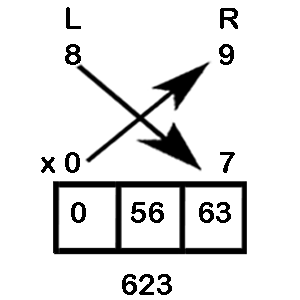
Step 1: We have to rewrite as 89 x 07 as both the numbers must have equal number of digits
Step 2: 89 x 07 = 0/56/63
Step 3: Now perform the carry over to obtain the final answer as 623
Exercises:
22 x 14 = 308
91 x 19 = 1729
77 x 23 = 1771
8.4 x 2.8 = 23.52
88 x 6 = 528
Now let us examine the multiplication of three digit numbers.
Example 1: 123 x 456
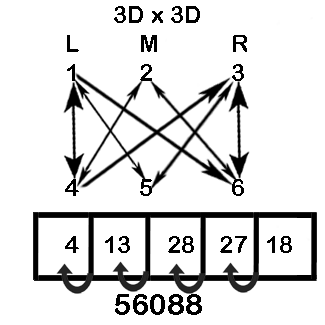
Step 1: Make five boxes
Step 2: L x L = 1 x 4 = 4
Step 3: L x M + M x L = 1 x 5 + 2 x 4 = 13
Step 4: L x R + R x L + M x M = 1 x 6 + 3 x 4 + 2 x 5 = 28 (note that we have crossed all three digits in this step)
Step 5: M x R + R x M = 2 x 6 + 3 x 5 = 27
Step 6: R x R = 3 x 6 = 18
Step 7: Perform the carry over to obtain the final answer as 56088
Example 2: 352 x 23

Step 1: Rewrite as 352 x 023
Step 2: 352 x 023 = 0/6/19/19/6
Step 3: Perform the carry over to obtain the final answer as 8096
Exercises:
304 x 212 = 64448
412 x 215 = 88580
342 x 214 = 73188
213 x 224 = 47712
324 x 225 = 72900
3.11 x 24.2 = 75.262
34.5 x 21.3 = 734.85
21.5 x 24.1 = 518.15
3.04 x 2.05 = 6.232
3.21 x 2.22 = 7.1262
344 x 21 = 7224
425 x 32 = 13600
523 x 52 = 27196
215 x 35 = 7525
204 x 55 = 11220
786 x 786 = 617796
Now let us examine the multiplication of four digit numbers.
Example: 1234 x 5678
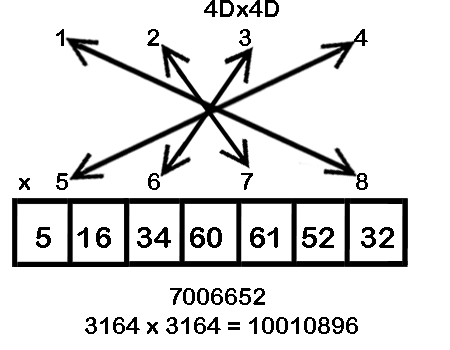
Step 1: Make 7 boxes
Step 2: Proceeding from the left side and moving towards the right side
Step 3: 1 x 5 = 5
Step 4: (1 x 6) + (2 x 5) = 16
Step 5: (1 x 7) + (3 x 5) + (2 x 6) = 34
Step 6: (1 x8) + (4 x5) + (2 x7) + (3x6) = 60 (Note that we have crossed all four digits in this critical step)
Step 7: (2 x 8) + (4 x 6) + (3 x 7) = 61
Step 8: (3 x 8) + (4 x 7) = 52
Step 9: 4 x 8 = 32
Inset the boxes: 5/16/34/60/61/52/32
Step 10: Perform the carryover to derive the final answer as 7006652
Exercises:
3164 x 3164 = 10010896
1021 x 2103 = 2147163
6471 x 6212 = 40197852
Course:


