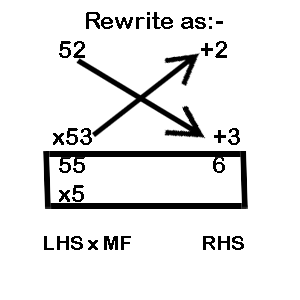
When neither the multiplicand nor the multiplier is sufficiently close to a convenient power of 10 than we can take a multiple of power of 10 and call it as the working base and then perform the necessary operation with its assistance. Example 1: 52 x 53 Step 1: Select the base as 50 = 10 x 5. We will call 5 as our multiplying factor (MF).
275/6 = 2756 Answer
Step 2: Proceeding as per Chapter 3 (Nikhilam) we obtain the RHS as 2 x 3 = 6 and LHS as (52 + 3) or (53 +2) = 55
Step 3: Now we have to multiply the LHS by the MF so 55 x 5 = 275 (This is a very important and critical step)
Step 4: Now combine the LHS and RHS to obtain the final answer as 2756
Note: In this method the carry over from RHS, if required, must be performed as the last step after multiplying the LHS by MF.
Example 2: 53 x 54
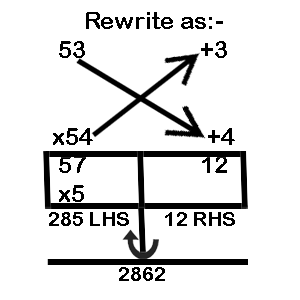
LHS = (53 + 4) or (54 + 3) = 57
RHS = 3 x 4 = 12
Multiply LHS by MF: 57 x 5 = 285
Carry over 1 from the right side and add to LHS (285 + 1 = 286) and obtain the final answer as 2862
Note: The rule of carry over states that the number of digits on the RHS is equal to the number of zeros in the base, is also applicable here.
Example 3: 67 x 68
B = 70 = 10 x 7
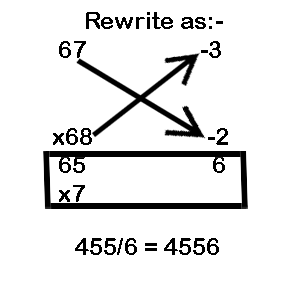
Take the base as 70 = 10 x 7 (Since both the numbers are closer to 70)
LHS = (67–2) or (68–3) =65
RHS = (-3) x (-2) = 6
Multiply LHS by MF: 65 x 7 = 455
Combine with RHS giving the final answer as 4556
Example 4: 203 x 204
B = 200 = 100 x 2
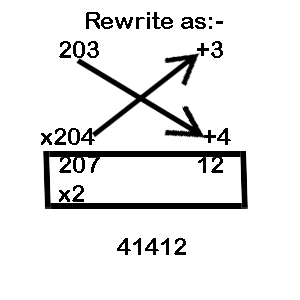
Take the base as 200 = 100 x 2
LHS: (203 + 4) or (204 + 3) = 207
RHS: 3 x 4 = 12
Multiple LHS by MF: 207 x 2 = 414
Combine with RHS to get the final answer as 41412
Example 5: 3003 x 3006
B = 3000 = 1000 x 3
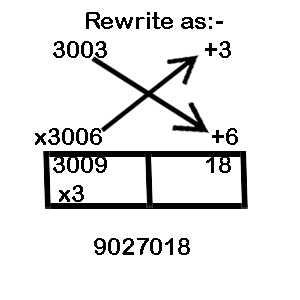
Take the base as 3000 = 1000 x 3
LHS (3003 + 6) or (3006 + 3) = 3009
RHS: 3 x 6 = 018 ( Note the base has three zeros so we need to add a preceding zero to make up 3 digits)
Multiply LHS by MF: 3009 x 3 = 9027
Combine LHS and RHS to derive the final answer as 9027018
Example 6: 52 x 48
B = 50 = 10 x 5
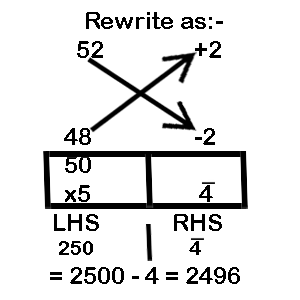
Taking the base as 50 = 10 x 5
LHS:(50 – 2) or (48 + 2) = 50
RHS = (+2) (-2) = -4
Multiply the LHS by MF: 50 x 5 = 250
Now increase one zero in LHS (As the base 50 has one zero) and then subtract the RHS from LHS to obtain the final answer. 2500 – 4 = 2496
Exercises:
21 x 23 = 483
59 x 59 = 3481
46 x 44 = 2024
62 x 58 = 3596
7.7 x 7.8 = 60.06 (Remember to convert to whole numbers before performing any calculations)
82 x 83 = 6806
505 x 506 = 255530
9009 x 9009 = 81162081
192 x 193 = 37056
202 x 198 = 39996
Course:


