Solution: More Trees in a Row Math Puzzle
Igor's Solution
This solution might sound too trivial or like "cheating" to most, but I call it taking advantage of the way the problem is written.
The original problem states: You have ten trees. Arrange them in four rows of five
Let's assume we arrange the trees in a "single" ten-tree row:
You can define a large number of unique rows. I give you four examples:
- A, B, C, D, E
- B, C, D, E, F
- C, D, E, F, G
- D, E, F, G, H
Now, nowhere in the problem does it say that you need to have equidistant rows, so you could also make a row by skipping trees, which increases the number of possible solutions. For example:
A, C, F, I, J
Finally, the problem never states that they have to be unique rows. This can yield infinite solutions. For example:
- A, B, C, D, E
- A, B, C, D, E
.
.
.
n. A, B, C, D, E
Lawrence excludes rows of trees that are colinear—three or more points are colinear if they are on the same straight line. The trees in a single row are colinear. Igor’s solution depends on having all the trees on one straight line, so they are all colinear. Lawrence doesn’t allow this, interpreting the problem to mean that each row of trees is on a different straight line.
Lawrence Explains
I will prove that this is not a valid problem in the Euclidean space as it has no solution.
First, let's define that no two rows of the four rows of trees are colinear. (Otherwise, it is not much of a problem.)
|
A) Let's form the first row of trees. By definition, we need five trees. We'll call this row A. We now have five trees left.
|
 |
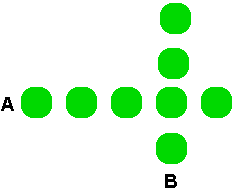 B) Let's form the second row of trees. Since this row cannot be colinear with row A, that means this row can have at most one tree shared with row A. We need at least four additional trees for this row. We'll call this row B. One tree left. (Can you sense the problem already?)
B) Let's form the second row of trees. Since this row cannot be colinear with row A, that means this row can have at most one tree shared with row A. We need at least four additional trees for this row. We'll call this row B. One tree left. (Can you sense the problem already?)
C) We are going to form the third row of trees. In order not to be colinear with A and B, we can only share at most one tree with A and one tree with B. We need at least three additional trees for this row. Oops, we only have one tree left.
Thus, this problem has no valid solution except in warped space.
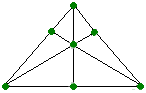 In our Trees in a Row Math Puzzle, we asked you to figure out how to plant seven trees in six rows of three trees each. Here is our solution.
In our Trees in a Row Math Puzzle, we asked you to figure out how to plant seven trees in six rows of three trees each. Here is our solution.
