Magic Stars

2	9	4
7	5	3
6	1	8

A 3 x 3 magic square with a solution

This puzzle explores the world of magic stars, similar in concept to magic squares.

We explored magic squares in Magic Squares and More Magic Squares. In those puzzles we tried to arrange all the numbers from 1 to 9 in the boxes of a 3 x 3 square so that all rows, columns, and diagonals add up to the same number. Here is one solution to a puzzle in which the numbers in every row, column, and diagonal add up to 15.

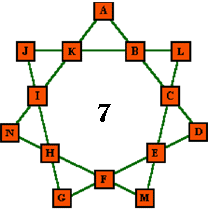
Magic stars take the magic squares concept and apply it to a star shape. Star 1 shows a magic star of order 5: a five-pointed star with a box at each vertex and intersection. There are 10 boxes altogether. Each has a letter in it. The problem: Is there any way to replace the letters A–H with numbers from 1 to 10 so that the sums of the number added along every line are the same. Each number may be used only once.

The “magic sum,” S, is found by adding all the numbers from 1 to 10. That sum is 55. When you add up all five lines in the star, you will get a sum that is 2 x 55, or 110 (because each number appears in exactly two different lines). Since the total of all the sums is 110 and there are five lines, the numbers along each line must sum to 110 / 5, or 22.

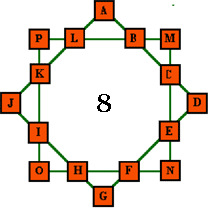
For each of the magic stars shown below, your challenge is to find a solution if one exists. One of the following magic stars has no solution. The others have many possible solutions. If there is no solution, can you show why? In each case you start by finding the magic sum, S, the amount that each line in the star must add up to. Solving these puzzles is a little bit like solving a sudoku puzzle. You start with one number and keep trying more numbers until you get to a contradiction. Then go back and try something else.

1. Magic star of order 5 (5 lines, numbers from 1 to 10)	2. Magic star of order 6 (6 lines, numbers from 1 to 12)

3. Magic star of order 7 (7 lines, numbers from 1 to 14)	4. Magic star of order 8 (8 lines, numbers from 1 to 16)

Background

Magic squares have been around and of interest to mathematicians for centuries. Magic stars represent a more modern form of combinatorics, and not as much is known about them. Magic stars come in many sizes and formats and tend to have many solutions. Mathematicians try to determine how many solutions exist for each type of magic star and how they are related. Some of this is discussed in master puzzler Martin Gardner’s book, Mathematical Carnival (Knopf, 1975). A number of Web sites are devoted to magic stars in all their many variations and intricacies. One of the best and most comprehensive is Magic Stars, created by Harvey Heinz. The graphics used for these problems were borrowed from Mr. Heinz with his permission from his Web site. If these problems intrigue you, check out the Web site.

Course:

Math
Algebra

Result/Solution(s)

Solution: Magic Stars Math Puzzle

1. Magic Star of Order 5

Surprise, surprise, the simplest magic star is the one with no solution. (If you tried to solve it, you probably figured that out by now.)

Here’s one way to think about it. Start with 1. First we need to show that if there is a solution, one of the lines with 1 in it must have a 10 in it as well. We can prove this by assuming that it doesn’t. Since the total is 22, the other three numbers must add up to 21.

Suppose we use 1 + 9 + 8 + 3. We need one more line with 1 + 7 + 6 + ?? The only number that works is 8—but 8 was already used.

Suppose the first row is 1 + 9 + 7 + 4, then the second row is 1 + 8 + 6 + ?? The only number that works is 7, but 7 was already used.

It won’t take long to exhaust all the possibilities that don’t have 1 and 10 in the same line. Both 1 and 10 must be in the same line.

Now start with 1 + 10. The next two numbers must add up to 11.

Here are all the possibilities for the first line passing through 1 and 10:

1a: 1 + 10 + 6 + 5

1b: 1 + 10 + 8 + 3

1c: 1 + 10 + 9 + 2

1d: 1 + 10 + 7 + 4

Here are all the possibilities for the second line through 1 (but not 10):

2a: 1 + 9 + 8 + 4

2b: 1 + 9 + 7 + 5

2c: 1 + 8 + 7 + 6

Here are all the possibilities for the third line through 10 (and not 1):

3a: 10 + 7 + 3 + 2

3b: 10 + 6 + 4 + 2

3c: 10 +5 + 4 + 3

Suppose we try 1a. Then the second line must be 2a. (2b and 2c include a 5 or 6, which was already used.) Unfortunately, 3b and 3c include a 6, or a 5, which are already used in line 1a. And 3a has no number in common with 2a. Since every line through 10, like lines 3a, 3b, and 3c, must cross line 2 somewhere, and there is no number in common in line 2a and 3a, the choice of line 1a is impossible.

If you work carefully through the numbers, you’ll see that the same is true for choosing lines 1b or 1c. Therefore, there is no solution for the level 5 magic star.

Actually there are other numbers, not 1–10, that will make a kind of magic star. See if you can make a magic 5-pointed star using numbers 1–6, 8, 9, 10, and 12. (First you’ll need to find the magic sum.) If you want to see an answer, check the Magic Stars Web site.

2. Magic Star of Order 6

There are many solutions for order 6 that use all the numbers from 1 to 12. The magic sum, S, is 26. Can you figure out why? Here is one solution. According to Harvey Heinz, mathematicians have proven that there are 80 possible solutions.

3. Magic Star of Order 7

According to Harvey Heinz, there are 72 possible solutions. Here is one of them.

4. Magic Star of Order 8

According to Harvey Heinz there are 112 possible solutions for magic stars of order 8. Here is one of them.

Acknowledgement: The graphics in this month’s math puzzle were created by Harvey Heinz and are used here with his permission.

Or log in with...

Puzzle