| |
Content |
Further guidance |
Links |
| 5.1 |
- Concepts of population, sample, random sample, discrete and continuous data.
- Presentation of data: frequency distributions (tables); frequency histograms with equal class intervals;
- box-and-whisker plots; outliers.
- Grouped data: use of mid-interval values for calculations; interval width; upper and lower interval boundaries; modal class.
Not required:
- frequency density histograms.
|
- Continuous and discrete data.
- Outlier is defined as more than 1.5 × IQR from the nearest quartile.
- Technology may be used to produce histograms and box-and-whisker plots.
|
- Appl: Psychology: descriptive statistics, random sample (various places in the guide).
- Aim 8: Misleading statistics.
- Int: The St Petersburg paradox, Chebychev, Pavlovsky.
|
| 5.2 |
- Statistical measures and their interpretations.
- Central tendency: mean, median, mode.
- Quartiles, percentiles.
- Dispersion: range, interquartile range, variance, standard deviation.
- Effect of constant changes to the original data.
- Applications.
|
- On examination papers, data will be treated as the population.
- Calculation of mean using formula and technology. Students should use mid-interval values to estimate the mean of grouped data.
- Calculation of standard deviation/variance using only technology.
Link to 2.3, transformations.
Examples:
- If 5 is subtracted from all the data items, then the mean is decreased by 5, but the standard deviation is unchanged.
- If all the data items are doubled, the median is doubled, but the variance is increased by a factor of 4.
|
- Appl: Psychology: descriptive statistics (various places in the guide).
- Appl: Statistical calculations to show patterns and changes; geographic skills; statistical graphs.
- Appl: Biology 1.1.2 (calculating mean and standard deviation ); Biology 1.1.4 (comparing means and spreads between two or more samples).
- Int: Discussion of the different formulae for variance.
- TOK: Do different measures of central tendency express different properties of the data? Are these measures invented or discovered? Could mathematics make alternative, equally true, formulae? What does this tell us about mathematical truths?
- TOK: How easy is it to lie with statistics?
|
| 5.3 |
Cumulative frequency; cumulative frequency graphs; use to find median, quartiles, percentiles. |
Values of the median and quartiles produced by technology may be different from those obtained from a cumulative frequency graph. |
. |
| 5.4 |
- Linear correlation of bivariate data.
- Pearson’s product–moment correlation coefficient r.
- Scatter diagrams; lines of best fit.
- Equation of the regression line of y on x.
- Use of the equation for prediction purposes.
- Mathematical and contextual interpretation.
Not required:
- the coefficient of determination R2.
|
- Independent variable x, dependent variable y.
- Technology should be used to calculate r. However, hand calculations of r may enhance understanding.
- Positive, zero, negative; strong, weak, no correlation.
- The line of best fit passes through the mean point.
- Technology should be used find the equation.
- Interpolation, extrapolation.
|
- Appl: Chemistry 11.3.3 (curves of best fit).
- Appl: Geography (geographic skills). Measures of correlation; geographic skills.
- Appl: Biology 1.1.6 (correlation does not imply causation).
- TOK: Can we predict the value of x from y, using this equation?
- TOK: Can all data be modelled by a (known) mathematical function? Consider the reliability and validity of mathematical models in describing real-life phenomena.
|
| 5.5 |
- Concepts of trial, outcome, equally likely outcomes, sample space (U) and event.
- The probability of an event
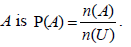
- The complementary events A and A′ (not A).
- Use of Venn diagrams, tree diagrams and tables of outcomes.
|
- The sample space can be represented diagrammatically in many ways.
- Experiments using coins, dice, cards and so on, can enhance understanding of the distinction between (experimental) relative frequency and (theoretical) probability.
- Simulations may be used to enhance this topic.
- Links to 5.1, frequency; 5.3, cumulative frequency.
|
TOK: To what extent does mathematics offer models of real life? Is there always a function to model data behaviour? |
| 5.6 |
- Combined events, P(A∪ B).
- Mutually exclusive events: P(A∩ B) = 0 .Conditional probability; the definition
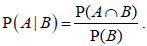
- Independent events; the definition P( A| B) = P(A) = P( A| B′) .
- Probabilities with and without replacement.
|
- The non-exclusivity of “or”.
- Problems are often best solved with the aid of a Venn diagram or tree diagram, without explicit use of formulae.
|
- Aim 8: The gambling issue: use of probability in casinos. Could or should mathematics help increase incomes in gambling?
- TOK: Is mathematics useful to measure risks?
- TOK: Can gambling be considered as an application of mathematics? (This is a good opportunity to generate a debate on the nature, role and ethics of mathematics regarding its applications.)
|
| 5.7 |
- Concept of discrete random variables and their probability distributions.
- Expected value (mean), E(X ) for discrete data.
- Applications.
|
- Simple examples only, such as:

- E(X ) = 0 indicates a fair game where X represents the gain of one of the players.
- Examples include games of chance.
|
. |
| 5.8 |
- Binomial distribution.
- Mean and variance of the binomial distribution.
Not required:
- formal proof of mean and variance.
|
Link to 1.3, binomial theorem.
- Conditions under which random variables have this distribution.
- Technology is usually the best way of calculating binomial probabilities.
|
. |
| 5.9 |
- Normal distributions and curves.
- Standardization of normal variables (z-values, z-scores).
- Properties of the normal distribution.
|
- Probabilities and values of the variable must be found using technology.
- Link to 2.3, transformations.
- The standardized value ( z ) gives the number of standard deviations from the mean.
|
- Appl: Biology 1.1.3 (links to normal distribution).
- Appl: Psychology: descriptive statistics (various places in the guide).
|