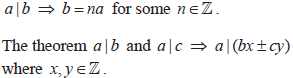Option: Discrete mathematics

PrintPrint
  Content Further guidance Links
10.1
  • Strong induction.
  • Pigeon-hole principle.
 For example, proofs of the fundamental theorem of arithmetic and the fact that a tree with n vertices has n – 1 edges.
  • TOK: Mathematics and knowledge claims. The difference between proof and conjecture, eg Goldbach’s conjecture. Can a mathematical statement be true before it is proven?
  • TOK: Proof by contradiction.
10.2
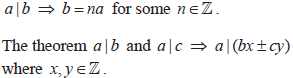  • Division and Euclidean algorithms.
  • The greatest common divisor, gcd(a,b) , and the least common multiple, lcm(a,b) , of integers a and b.
  • Prime numbers; relatively prime numbers and the fundamental theorem of arithmetic.
  • The division algorithm a = bq + r , 0 ≤ r < b .
  • The Euclidean algorithm for determining the greatest common divisor of two integers.
  • Int: Euclidean algorithm contained in Euclid’s Elements, written in Alexandria about 300 BCE.
  • Aim 8: Use of prime numbers in cryptography. The possible impact of the discovery of powerful factorization techniques on internet and bank security.
10.3 Linear Diophantine equations ax + by = c . General solutions required and solutions subject to constraints. For example, all solutions must be positive. Int: Described in Diophantus’ Arithmetica written in Alexandria in the 3rd century CE. When studying Arithmetica, a French mathematician, Pierre de Fermat (1601–1665) wrote in the margin that he had discovered a simple proof regarding higher-order Diophantine equations—Fermat’s last theorem.
10.4
  • Modular arithmetic.
  • The solution of linear congruences.
  • Solution of simultaneous linear congruences (Chinese remainder theorem).
   Int: Discussed by Chinese mathematician Sun Tzu in the 3rd century CE.
10.5 Representation of integers in different bases. On examination papers, questions that go beyond base 16 will not be set. Int: Babylonians developed a base 60 number system and the Mayans a base 20 number system.
10.6 Fermat’s little theorem. ap = a (mod p) , where p is prime. TOK: Nature of mathematics. An interest may be pursued for centuries before becoming “useful”.
10.7
  • Graphs, vertices, edges, faces. Adjacent vertices, adjacent edges.
  • Degree of a vertex, degree sequence.
  • Handshaking lemma.
  • Simple graphs; connected graphs; complete graphs; bipartite graphs; planar graphs; trees; weighted graphs, including tabular representation.
  • Subgraphs; complements of graphs.
  • Euler’s relation: v − e + f = 2 ; theorems for planar graphs including e ≤ 3v − 6 , e ≤ 2v − 4 ,leading to the results that K5 and K3,3 planar.
  • Two vertices are adjacent if they are joined by an edge. Two edges are adjacent if they have a common vertex.
  • It should be stressed that a graph should not be assumed to be simple unless specifically stated. The term adjacency table may be used.
  • If the graph is simple and planar and v ≥ 3 , then e ≤ 3v − 6 .
  • If the graph is simple, planar, has no cycles of length 3 and v ≥ 3 , then e ≤ 2v − 4 .
  • Aim 8: Symbolic maps, eg Metro and Underground maps, structural formulae in chemistry, electrical circuits.
  • TOK: Mathematics and knowledge claims. Proof of the four-colour theorem. If a theorem is proved by computer, how can we claim to know that it is true?
  • Aim 8: Importance of planar graphs in constructing circuit boards.
  • TOK: Mathematics and knowledge claims. Applications of the Euler characteristic (v − e + f ) to higher dimensions. Its use in understanding properties of shapes that cannot be visualized.
10.8
  • Walks, trails, paths, circuits, cycles.
  • Eulerian trails and circuits.
  • Hamiltonian paths and cycles.
  • A connected graph contains an Eulerian circuit if and only if every vertex of the graph is of even degree.
  • Simple treatment only.
 Int: The “Bridges of Königsberg” problem.
10.9 Graph algorithms: Kruskal’s; Dijkstra’s. . .
10.10 Chinese postman problem.
Not required:
  • Graphs with more than four vertices of odd degree.
  • Travelling salesman problem.
  • Nearest-neighbour algorithm for determining an upper bound.
  • Deleted vertex algorithm for determining a lower bound.
  • To determine the shortest route around a weighted graph going along each edge at least once
  • To determine the Hamiltonian cycle of least weight in a weighted complete graph

.
  • Int: Problem posed by the Chinese mathematician Kwan Mei-Ko in 1962.
  • TOK: Mathematics and knowledge claims. How long would it take a computer to test all Hamiltonian cycles in a complete, weighted graph with just 30 vertices?
10.11
  • Recurrence relations. Initial conditions,recursive definition of a sequence.
  • Solution of first- and second-degree linear homogeneous recurrence relations with constant coefficients.
  • The first-degree linear recurrence relation Modelling with recurrence relations un aun-1 +b .
  • Includes the cases where auxiliary equation has equal roots or complex roots.
  • Solving problems such as compound interest,debt repayment and counting problems.
 TOK: Mathematics and the world. The connections of sequences such as the Fibonacci sequence with art and biology.

Previous page

Quick Links

Communities

Subjects

Roles

About Hootsgo