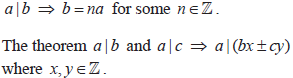| |
Content |
Further guidance |
Links |
| 10.1 |
- Strong induction.
- Pigeon-hole principle.
|
For example, proofs of the fundamental theorem of arithmetic and the fact that a tree with n vertices has n – 1 edges. |
- TOK: Mathematics and knowledge claims. The difference between proof and conjecture, eg Goldbach’s conjecture. Can a mathematical statement be true before it is proven?
- TOK: Proof by contradiction.
|
| 10.2 |
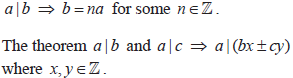 - Division and Euclidean algorithms.
- The greatest common divisor, gcd(a,b) , and the least common multiple, lcm(a,b) , of integers a and b.
- Prime numbers; relatively prime numbers and the fundamental theorem of arithmetic.
|
- The division algorithm a = bq + r , 0 ≤ r < b .
- The Euclidean algorithm for determining the greatest common divisor of two integers.
|
- Int: Euclidean algorithm contained in Euclid’s Elements, written in Alexandria about 300 BCE.
- Aim 8: Use of prime numbers in cryptography. The possible impact of the discovery of powerful factorization techniques on internet and bank security.
|
| 10.3 |
Linear Diophantine equations ax + by = c . |
General solutions required and solutions subject to constraints. For example, all solutions must be positive. |
Int: Described in Diophantus’ Arithmetica written in Alexandria in the 3rd century CE. When studying Arithmetica, a French mathematician, Pierre de Fermat (1601–1665) wrote in the margin that he had discovered a simple proof regarding higher-order Diophantine equations—Fermat’s last theorem. |
| 10.4 |
- Modular arithmetic.
- The solution of linear congruences.
- Solution of simultaneous linear congruences (Chinese remainder theorem).
|
|
Int: Discussed by Chinese mathematician Sun Tzu in the 3rd century CE. |
| 10.5 |
Representation of integers in different bases. |
On examination papers, questions that go beyond base 16 will not be set. |
Int: Babylonians developed a base 60 number system and the Mayans a base 20 number system. |
| 10.6 |
Fermat’s little theorem. |
ap = a (mod p) , where p is prime. |
TOK: Nature of mathematics. An interest may be pursued for centuries before becoming “useful”. |
| 10.7 |
- Graphs, vertices, edges, faces. Adjacent vertices, adjacent edges.
- Degree of a vertex, degree sequence.
- Handshaking lemma.
- Simple graphs; connected graphs; complete graphs; bipartite graphs; planar graphs; trees; weighted graphs, including tabular representation.
- Subgraphs; complements of graphs.
- Euler’s relation: v − e + f = 2 ; theorems for planar graphs including e ≤ 3v − 6 , e ≤ 2v − 4 ,leading to the results that K5 and K3,3 planar.
|
- Two vertices are adjacent if they are joined by an edge. Two edges are adjacent if they have a common vertex.
- It should be stressed that a graph should not be assumed to be simple unless specifically stated. The term adjacency table may be used.
- If the graph is simple and planar and v ≥ 3 , then e ≤ 3v − 6 .
- If the graph is simple, planar, has no cycles of length 3 and v ≥ 3 , then e ≤ 2v − 4 .
|
- Aim 8: Symbolic maps, eg Metro and Underground maps, structural formulae in chemistry, electrical circuits.
- TOK: Mathematics and knowledge claims. Proof of the four-colour theorem. If a theorem is proved by computer, how can we claim to know that it is true?
- Aim 8: Importance of planar graphs in constructing circuit boards.
- TOK: Mathematics and knowledge claims. Applications of the Euler characteristic (v − e + f ) to higher dimensions. Its use in understanding properties of shapes that cannot be visualized.
|
| 10.8 |
- Walks, trails, paths, circuits, cycles.
- Eulerian trails and circuits.
- Hamiltonian paths and cycles.
|
- A connected graph contains an Eulerian circuit if and only if every vertex of the graph is of even degree.
- Simple treatment only.
|
Int: The “Bridges of Königsberg” problem. |
| 10.9 |
Graph algorithms: Kruskal’s; Dijkstra’s. |
. |
. |
| 10.10 |
Chinese postman problem.
Not required:
- Graphs with more than four vertices of odd degree.
- Travelling salesman problem.
- Nearest-neighbour algorithm for determining an upper bound.
- Deleted vertex algorithm for determining a lower bound.
|
- To determine the shortest route around a weighted graph going along each edge at least once
- To determine the Hamiltonian cycle of least weight in a weighted complete graph
. |
- Int: Problem posed by the Chinese mathematician Kwan Mei-Ko in 1962.
- TOK: Mathematics and knowledge claims. How long would it take a computer to test all Hamiltonian cycles in a complete, weighted graph with just 30 vertices?
|
| 10.11 |
- Recurrence relations. Initial conditions,recursive definition of a sequence.
- Solution of first- and second-degree linear homogeneous recurrence relations with constant coefficients.
- The first-degree linear recurrence relation Modelling with recurrence relations un aun-1 +b .
|
- Includes the cases where auxiliary equation has equal roots or complex roots.
- Solving problems such as compound interest,debt repayment and counting problems.
|
TOK: Mathematics and the world. The connections of sequences such as the Fibonacci sequence with art and biology. |