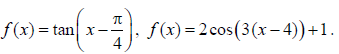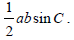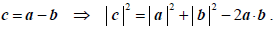| |
Content |
Further guidance |
Links |
| 3.1 |
The circle: radian measure of angles; length of an arc; area of a sector. |
Radian measure may be expressed as exact multiples of π , or decimals. |
- Int: Seki Takakazu calculating π to ten decimal places.
- Int: Hipparchus, Menelaus and Ptolemy.
- Int: Why are there 360 degrees in a complete turn? Links to Babylonian mathematics.
- TOK: Which is a better measure of angle: radian or degree? What are the “best” criteria by which to decide?
- TOK: Euclid’s axioms as the building blocks of Euclidean geometry. Link to non-Euclidean geometry.
|
| 3.2 |
- Definition of cosθ and sinθ in terms of the unit circle.
- Definition of
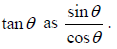
- Exact values of trigonometric ratios of
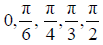 and their multiples. and their multiples.
|
- The equation of a straight line through the origin is y = x tanθ
- Examples:
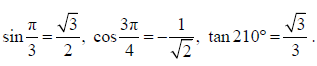
|
- Aim 8: Who really invented “Pythagoras’ theorem”?
- Int: The first work to refer explicitly to the sine as a function of an angle is the Aryabhatiya of Aryabhata (ca. 510).
- TOK: Trigonometry was developed by successive civilizations and cultures. How is mathematical knowledge considered from a sociocultural perspective?
|
| 3.3 |
- The Pythagorean identity cos2 θ + sin2 θ = 1.Double angle identities for sine and cosine.
- Relationship between trigonometric ratios.
|
- Simple geometrical diagrams and/or technology may be used to illustrate the double angle formulae (and other trigonometric identities).
Examples:
- Given sinθ , finding possible values of tanθ without finding θ .
- Given
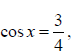 and x is acute, find sin2x without finding x. and x is acute, find sin2x without finding x.
|
. |
| 3.4 |
- The circular functions sin x , cos x and tan x : their domains and ranges; amplitude, their periodic nature; and their graphs.
- Composite functions of the form f (x) = asin (b(x + c) ) + d .
- Transformations.
- Applications.
|
- Examples:
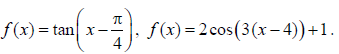
- Example: y = sinx used to obtain y = 3sin2x by a stretch of scale factor 3 in the y-direction and a stretch of scale factor 1/2 in the x-direction.
- Link to 2.3, transformation of graphs.
- Examples include height of tide, motion of a Ferris wheel.
|
Appl: Physics 4.2 (simple harmonic motion). |
| 3.5 |
- Solving trigonometric equations in a finite interval, both graphically and analytically.
- Equations leading to quadratic equations in sin x, cos x or tan x
. Not required:
- the general solution of trigonometric equations.
|
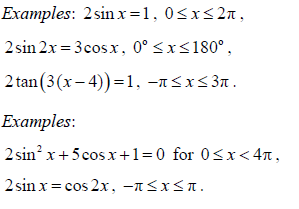 |
|
| 3.6 |
- Solution of triangles.
- The cosine rule.
- The sine rule, including the ambiguous case.
- Area of a triangle,
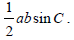
- Applications.
|
- Pythagoras’ theorem is a special case of the cosine rule.
- Link with 4.2, scalar product, noting that:
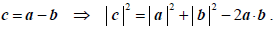
- Examples include navigation, problems in two and three dimensions, including angles of elevation and depression.
|
- Aim 8: Attributing the origin of a mathematical discovery to the wrong mathematician.
- Int: Cosine rule: Al-Kashi and Pythagoras.
- TOK: Non-Euclidean geometry: angle sum on a globe greater than 180°.
|
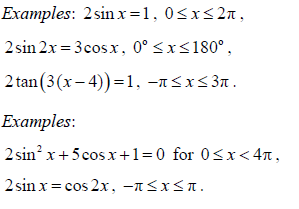


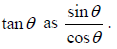
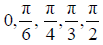 and their multiples.
and their multiples.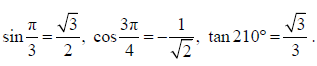
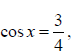 and x is acute, find sin2x without finding x.
and x is acute, find sin2x without finding x.