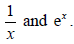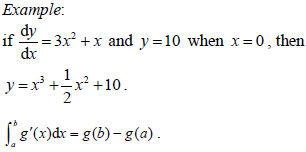| |
Content |
Further guidance |
Links |
| 6.1 |
- Informal ideas of limit and convergence.
- Limit notation.
- Definition of derivative from first principles as
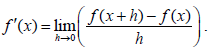
- Derivative interpreted as gradient function and as rate of change.
- Tangents and normals, and their equations.
Not required:
- analytic methods of calculating limits.
|
Example: 0.3, 0.33, 0.333, ... converges to 1/3
.Technology should be used to explore ideas of limits, numerically and graphically.
Example: 
- Links to 1.1, infinite geometric series; 2.5–2.7, rational and exponential functions, and asymptotes.
- Use of this definition for derivatives of simple polynomial functions only.
- Technology could be used to illustrate other derivatives.
Link to 1.3, binomial theorem.
- Use of both forms of notation,
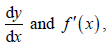
- for the first derivative.
- Identifying intervals on which functions are increasing or decreasing.
- Use of both analytic approaches and technology.
- Technology can be used to explore graphs and their derivatives.
|
- Appl: Economics 1.5 (marginal cost, marginal revenue, marginal profit).
- Appl: Chemistry 11.3.4 (interpreting the gradient of a curve).
- Aim 8: The debate over whether Newton or Leibnitz discovered certain calculus concepts.
- TOK: What value does the knowledge of limits have? Is infinitesimal behaviour applicable to real life?
- TOK: Opportunities for discussing hypothesis formation and testing, and then the formal proof can be tackled by comparing certain cases, through an investigative approach.
|
| 6.2 |
- Derivative of
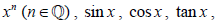 ex and ln x . ex and ln x .
- Differentiation of a sum and a real multiple of these functions.
- The chain rule for composite functions.
- The product and quotient rules.
- The second derivative.
- Extension to higher derivatives.
|
- Link to 2.1, composition of functions.
- Technology may be used to investigate the chain rule.
- Use of both forms of notation,

|
|
| 6.3 |
- Local maximum and minimum points. Testing for maximum or minimum.
- Points of inflexion with zero and non-zero gradients.
- Graphical behaviour of functions, including the relationship between the graphs of f , f ′ and f ′′ .
- Optimization.
- Applications.
Not required:
- points of inflexion where f ′′(x) is not defined: for example, y = x13 at (0,0).
|
- Using change of sign of the first derivative and using sign of the second derivative.
- Use of the terms “concave-up” for f ′′(x) > 0 ,and “concave-down” for f ′′(x) < 0 .
- At a point of inflexion , f ′′(x) = 0 and changes sign (concavity change).
- f ′′(x) = 0 is not a sufficient condition for a point of inflexion: for example, y = x4 at (0,0) .
- Both “global” (for large |x| ) and “local” behaviour.
- Technology can display the graph of a derivative without explicitly finding an expression for the derivative.
- Use of the first or second derivative test to justify maximum and/or minimum values.
- Examples include profit, area, volume.
- Link to 2.2, graphing functions.
|
Appl: profit, area, volume. |
| 6.4 |
- Indefinite integration as anti-differentiation.
- Indefinite integral of
 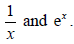
- The composites of any of these with the linear function ax + b .
- Integration by inspection, or substitution of the form ∫ f (g(x))g '(x)dx .
|
.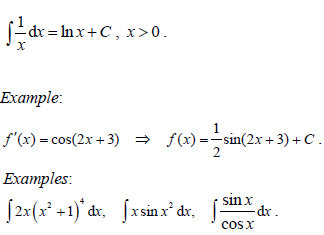 |
. |
| 6.5 |
- Anti-differentiation with a boundary condition to determine the constant term.
- Definite integrals, both analytically and using technology.
- Areas under curves (between the curve and the x-axis).
- Areas between curves.
- Volumes of revolution about the x-axis.
|
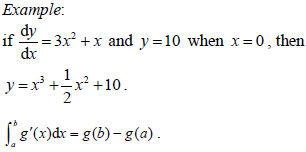 - The value of some definite integrals can only be found using technology.
- Students are expected to first write a correct expression before calculating the area.
- Technology may be used to enhance understanding of area and volume.
|
- Int: Successful calculation of the volume of the pyramidal frustum by ancient Egyptians (Egyptian Moscow papyrus).
- Use of infinitesimals by Greek geometers.
- Accurate calculation of the volume of a cylinder by Chinese mathematician Liu Hui
- Int: Ibn Al Haytham: first mathematician to calculate the integral of a function, in order to find the volume of a paraboloid.
|
| 6.6 |
- Kinematic problems involving displacement s, velocity v and acceleration a.
- Total distance travelled.
|
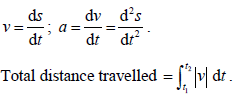 |
Appl: Physics 2.1 (kinematics). |
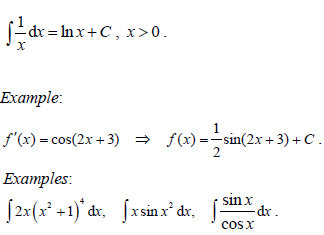


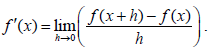

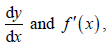
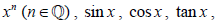 ex and ln x .
ex and ln x .