| |
Content |
Further guidance |
Links |
| 6.1 |
- Informal ideas of limit, continuity and convergence.
- Definition of derivative from first principles
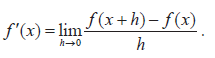
- The derivative interpreted as a gradient function and as a rate of change.
- Finding equations of tangents and normals.
- Identifying increasing and decreasing functions.
- The second derivative. Higher derivatives.
|
- Include result
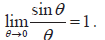
- Link to 1.1.
- Use of this definition for polynomials only.
- Link to binomial theorem in 1.3.
- Both forms of notation,
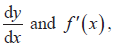 for the dx first derivative. for the dx first derivative.
- Use of both algebra and technology. d2 y
- Both forms of notation,
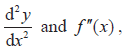 for the second derivative. for the second derivative.
- Familiarity with the notation
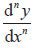 and f (n) (x) . Link with induction in 1.4. and f (n) (x) . Link with induction in 1.4.
|
- TOK: The nature of mathematics. Does the fact that Leibniz and Newton came across the calculus at similar times support the argument that mathematics exists prior to its discovery?
- Int: How the Greeks’ distrust of zero meant that Archimedes’ work did not lead to calculus.
- Int: Investigate attempts by Indian mathematicians (500–1000 CE) to explain division by zero.
- TOK: Mathematics and the knower. What does the dispute between Newton and Leibniz tell us about human emotion and mathematical discovery?
- Appl: Economics HL 1.5 (theory of the firm); Chemistry SL/HL 11.3.4 (graphical techniques); Physics SL/HL 2.1 (kinematics).
|
| 6.2 |
- Derivatives of xn , sin x , cos x , tan x , ex and ln x .
- Differentiation of sums and multiples of functions.
- The product and quotient rules.
- The chain rule for composite functions. Related rates of change.
- Implicit differentiation.
- Derivatives of sec x , csc x , cot x , ax , loga x ,arcsin x , arccos x and arctan x
|
. |
- Appl: Physics HL 2.4 (uniform circular motion); Physics 12.1 (induced electromotive force (emf)).
- TOK: Mathematics and knowledge claims. Euler was able to make important advances in mathematical analysis before calculus had been put on a solid theoretical foundation by Cauchy and others. However, some work was not possible until after Cauchy’s work. What does this tell us about the importance of proof and the nature of mathematics?
- TOK: Mathematics and the real world. The seemingly abstract concept of calculus allows us to create mathematical models that permit human feats, such as getting a man on the Moon. What does this tell us about the links between mathematical models and physical reality?
|
| 6.3 |
- Local maximum and minimum values. Optimization problems.
- Points of inflexion with zero and non-zero gradients.
- Graphical behaviour of functions, including the relationship between the graphs of f, f' and f"
Not required:
- Points of inflexion, where f ′′(x) is not defined, for example, y = x1/ 3 at (0, 0) .
|
- Testing for the maximum or minimum using the change of sign of the first derivative and using the sign of the second derivative.
- Use of the terms “concave up” for f ′′(x) > 0 , “concave down” for f ′′(x) < 0 .
- At a point of inflexion, f ′′(x) = 0 and changes sign (concavity change).
|
. |
| 6.4 |
- Indefinite integration as anti-differentiation.
- Indefinite integral of xn , sin x , cos x and ex .
- Other indefinite integrals using the results from 6.2.
- The composites of any of these with a linear function.
|
- Indefinite integral interpreted as a family of curves.
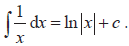
- Examples include
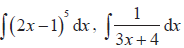 and and 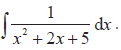
|
. |
| 6.5 |
- Anti-differentiation with a boundary condition to determine the constant of integration.
- Definite integrals.
- Area of the region enclosed by a curve and the x-axis or y-axis in a given interval; areas of regions enclosed by curves.
- Volumes of revolution about the x-axis or y-axis.
|
The value of some definite integrals can only be found using technology. |
|
| 5.6 |
- Kinematic problems involving displacement s, velocity v and acceleration a.
- Total distance travelled.
|
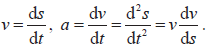 Total distance travelled = Total distance travelled = 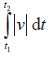 . .
|
- Appl: Physics HL 2.1 (kinematics).
- Int: Does the inclusion of kinematics as core mathematics reflect a particular cultural heritage? Who decides what is mathematics?
|
| 6.7 |
- Integration by substitution
- Integration by parts.
|
- On examination papers, non-standard substitutions will be provided.
- Link to 6.2.
- Examples:
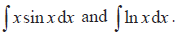
- Repeated integration by parts.
- Examples:

|
. |