| |
Content |
Further guidance |
Links |
| 1.1 |
- Arithmetic sequences and series; sum of finite arithmetic series; geometric sequences and series; sum of finite and infinite geometric series.
- Sigma notation.
- Applications.
|
- Technology may be used to generate and display sequences in several ways.
- Link to 2.6, exponential functions.
- Examples include compound interest and population growth.
|
- Int: The chess legend (Sissa ibn Dahir).
- Int: Aryabhatta is sometimes considered the “father of algebra”. Compare with al-Khawarizmi.
- TOK: How did Gauss add up integers from 1 to 100? Discuss the idea of mathematical intuition as the basis for formal proof.
- TOK: Debate over the validity of the notion of “infinity”: finitists such as L. Kronecker consider that “a mathematical object does not exist unless it can be constructed from natural numbers in a finite number of steps”.
- TOK: What is Zeno’s dichotomy paradox? How far can mathematical facts be from intuition?
|
| 1.2 |
- Elementary treatment of exponents and logarithms.
- Laws of exponents; laws of logarithms.
- Change of base.
|

|
- Appl: Chemistry 18.1 (Calculation of pH ).
- TOK: Are logarithms an invention or discovery? (This topic is an opportunity for teachers to generate reflection on “the nature of mathematics”.)
|
| 1.3 |
- The binomial theorem:
- expansion of (a + b), n∈N .
- Calculation of binomial coefficients using Pascal’s triangle and
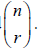
Not required:
- formal treatment of permutations and formula for nPr.
|
- Counting principles may be used in the development of the theorem.
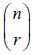 should be found using both the formula and technology. should be found using both the formula and technology.- Example: finding
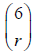 from inputting y = 6n Cr X and then reading coefficients from r the table. from inputting y = 6n Cr X and then reading coefficients from r the table.
- Link to 5.8, binomial distribution.
|
- Aim 8: Pascal’s triangle. Attributing the origin of a mathematical discovery to the wrong mathematician.
- Int: The so-called “Pascal’s triangle” was known in China much earlier than Pascal.
|