To start with, we have to figure out how much stone is in the Pyramids. Although there is a small amount of open space inside each Pyramid for the Pharaoh and his stuff, this is tiny compared with the overall volume. For this puzzle we can assume the Pyramids to be solid stone.
The formula for the volume of a pyramid is
V = 1/3 x H x Ab
where V is volume, H is the height of the pyramid, and Ab is the area of the base. Starting with Kheops, the square base is 230 m on a side, so the area is 52,900 sq m (20,425 sq yd). The height is 146 m. So
V = 1/3 x 146 x 52,900 = 2,574,467 cu m (3,367,277 cu yd)
Following the same procedure we find that the volume of Khephren is 2,203,392 cu m (2,881,929 cu yd) and the volume of Mykerinos is 256,608 cu m (335,631 cu yd). The total volume of the three Pyramids is 5,034,467 cu m (6,584,836 cu yd).
Now let’s look at Napoleon’s proposed wall. How much stone would be needed to build a section 1 km (.6 mi) long? The volume of such a rectangle is Height x Length x Width. The Length is 1 km, or 1,000 m. The Height is 3 m and the Width is 30 cm, or 0.3 m. So
V = 1,000 x 3 x 0.3 = 900 cu m
Every 900 cu m of stone makes a wall 1 km long. Dividing the total volume of the stone in the Pyramids by the amount of stone in a 1-km section gives us the length, in kilometers, of the wall that could be built.
Length of Napoleon’s proposed wall around France = 5,034,467 / 900 = 5,594 km. Is that enough to go all the way around the country?
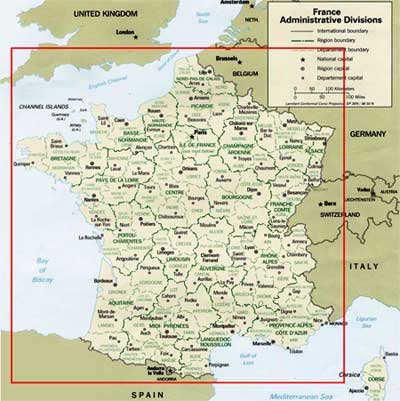
Courtesy of The General Libraries, The University of Texas at Austin
The red square around this map of France is 1,000 km (620 mi) on a side. The perimeter is 4,000 km (2,480 mi). So we’ve built a wall around France with 1,594 km (990 mi) of stone wall to spare.
But this is probably not what Napoleon had in mind. What if the wall followed the coastline and the boundaries with neighboring countries? Would there be enough stone for such a wall? We can’t answer that because we can’t know how long the boundary is. This may seem surprising, but the length of the boundary depends on how big a ruler you use to measure it. The smaller the ruler, the longer the path.


