Boxes, Cubes, and Nets

Previous math puzzles focused on polyominoes. This puzzle takes polyominoes into the third dimension.

Polyominoes are shapes made by attaching a certain number of squares of the same size so they line up along their edges. A polyomino can contain any number of squares, but shapes that use a fixed number of squares have a specific prefix that describes their number. Pentominoes are made of exactly five squares, hexominoes of six squares, and so forth. For more background about polyominoes and some intriguing polyomino puzzles, check out our Polyominoes and Polyomino Puzzles math puzzles.

Here are some sample pentominoes, and their names.

Monomino

Domino

Tromino

Tetromino

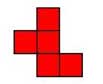Pentomino

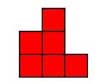Hexomino

There are several different ways to form each type of polyomino—the higher the number of squares, the more ways to form pentominoes with that many squares. In Polyominoes and Polyomino Puzzles, our math puzzles were concerned with finding all possible pentominoes, and with solving polyomino puzzles, jigsaw puzzles that use polyominoes as pieces to fill in a particular shape.

This month’s puzzle gives pentominoes and hexominoes a new dimension—literally. Suppose you take a cube-shaped box. Let’s start with one without a top, like the one shown here.

net

If you take a pair of scissors and carefully cut the box along all of its vertical edges, the shape can be flattened out to form a pentomino. This particular pentomino is sometimes called a cross pentomino or an X-pentomino because the five squares form a perfect symmetrical cross or X shape.

A flat shape that can be folded into a three-dimensional shape without cutting into it is called a net.

Puzzle 1

Here’s the first puzzle. You are to find all the different pentominoes that form nets for open-top cube boxes. Not all pentominoes are nets for cube boxes. For instance the I-shaped pentomino (right) cannot be folded into a box. Can you see why? (The squares marked "X" would overlap, and the result would be a square "tube" with no bottom or top.)

Your challenge: find all the different pentominoes that are nets for open-top cube boxes. How will you know when you’ve found them all? Well, there are 12 different pentominoes all together. (If you want to see them all, they can be found in the solution to the Polyominoes puzzle. If you want to find them all yourself, that’s fine too.) Some of these are nets; others are not. Your task is to decide which ones are the nets.

We recommend that you actually draw your pentominoes on graph paper, cut them out, and fold them to verify that they will indeed form an open box.

Finally, for every pentomino that cannot form a net for an open box, you should explain how you know it can’t be such a net.

Remember, two pentominoes may look different but still be the same shape if they are congruent to each other. Pentomino A in the figure below can be picked up, flipped over, and rotated so that it fits exactly on top of pentomino B. This is one way to show that they are congruent.

Puzzle 2

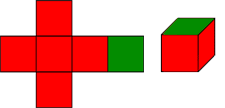
Your second challenge is to step up to hexominoes and nets for closed cubes. Remember, hexominoes are made from six attached squares. Find all the different hexominoes that are nets for a closed cube. One example is shown in the figure below. You can think of this hexomino as the X-pentomino with one added square. The added square folds over to close up the top of the cube.

Unfortunately, there are 35 different hexominoes. It would be tedious to find them all and prove which ones can and cannot be nets for cubes. However, there is a good shortcut that can save you a lot of trouble.

A net for a cube can only be made by adding a square to a pentomino that is a net for a net for an open-top cube box. Can you convince yourself that this is true? Take any pentomino that cannot form a net for a box. Can you find any way to add a square to it and make a net for a cube? Try it using the I-pentomino. We already know that it can’t form an open box. Can you add a square to it in any way that will allow it to fold into a cube?

net

Background

First, a couple of definitions. A polygon is a closed two-dimensional shape whose edges are straight lines that do not cross each other. A polyhedron is a closed three-dimensional shape whose faces are polygons.

Two-dimensional and three-dimensional geometry are often studied as if they were different subjects. In future puzzles, we study one way they are related—through the construction of nets, two-dimensional shapes made of polygons that fold up into polyhedrons.

This puzzle makes use of three other important mathematical ideas. The first of these is the concept of congruence, introduced above. Mathematically, two shapes are congruent if they have the same size and shape, regardless of their orientation. If you can pick up one of the shapes and rotate it, flip it over, and/or slide it so that it fits exactly on top of the other shapes, then the two shapes are congruent. This is one simple test for congruence. There are many others.

The second is the idea that you sometimes have to test to be sure whether two mathematical objects are the same or different. Just because two polyominoes look different, you can’t be sure they are different until you’ve picked one up and made sure it’s not congruent to the other. For polyominoes, congruence is the test—but mathematicians have many other tests they can use for different types of problems.

The third is the idea of finding all possible ways to solve a particular problem. This is a common type of problem in combinatorics. For example, find all the possible ways to arrange the numbers from 1 to N. Or for a more everyday example, a restaurant serves pizza with four different toppings: onions, mushrooms, sausages, and extra cheese. How many different types of pizzas can they make using 1, 2, 3, or 4 of the toppings? (Of course, a real restaurant would probably provide many more than four toppings.)

Combinatorics problems involving geometry can be much more complex. For example, if N is the number of faces in a polyhedron, there is no known rule or formula that can tell you how many different nets can be constructed for a polyhedron with N faces. (Mathematicians have worked out the exact number of nets for many different polyhedrons, but no general rule has ever been found.)

Course:

Math

Result/Solution(s)

Puzzle 1

For this puzzle you needed to figure out how many different pentominoes will fold up to make an open box?

There are 12 different pentominoes. Eight of them can be folded into open boxes. Four cannot. How can you decide which ones work and which don’t. For most of us, the surest way is to cut out the shapes and fold them to see if two of the squares overlap. On the other hand, some people can visualize the folding process without actually folding. And some people can visualize folding some of the shapes and not others.

Here are the 12 pentominoes, divided into those that work and those that don’t.

pentominoes

These don’t work. The squares marked with an “X” overlap when the shape is folded. Therefore the shape does not fold into an open box. The pentomino at the lower left cannot be folded properly because four of the squares are connected on two different sides.

The next eight pentominoes do work. They can all be folded to make open boxes. Cut them out and try folding them if you can convince yourself by visualizing.

pentominoes

Puzzle 2

This time you needed to find all the hexominoes that are nets for closed cubes; that is, find all the shapes made of six squares that fold into a cube.

This is a much harder problem because there are 35 different hexominoes and it would be tedious to find and test them all, so we make use of a shortcut.

Any pentomino that does not make an open box can’t be made into a cube by adding one more square. So we can start by adding a square to one of the eight pentominoes that make nets for open boxes. Since there are eight pentominoes to start from, and many ways to add a square to each one, you might think there are a large number of possibilities, but most of the possibilities are congruent to others.

Here’s a starting point. Any hexomino with four squares in a row and one square on each side is a net for a cube. For example, starting from the L-pentomino we can form four different nets in this way. Let’s label each one so we can keep track of them and refer back to them.


N1	N2	N3	N4

One more pentomino includes a strip of four and gives us two more nets.


	N5	N6

So now we’ve got six. How many more can we find? At this point we can rule out several possibilities.

Any hexomino with a strip of three or four squares and two squares on the same side of the strip can’t form a net. The squares marked X will overlap when the shape is folded.

pentominoes

Also, any hexomino with four squares forming a larger square also can be ruled out. The shape can’t be folded.

pentominoes

If you think a little, you’ll see that neither the X- nor the T-pentomino can form a net that we don’t already have. So out of our eight pentominoes we have four more that might form nets. We’ll have to think carefully about each one.

pentominoes

Starting from the first one, we can rule out several possibilities. The first two are congruent to nets that we already have, N2 and N6; the last four are impossible.


	N2	N6

But what about these? We have to consider each one:


	N7	N8

The first one can be ruled out because it contains one of the pentominoes that cannot form a net for an open box—so it can’t be a net for a cube. However, the next two can be folded into nets for a cube, so we’ve got two more, N7 and N8.

Now using the second unused pentomino, we can again rule out two because they include a square of four squares.

pentominoes

But we need to carefully consider each of the following. The first is congruent to N7. The second does not work. The squares marked with an X overlap when folded. The third gives us a new net, N9.


N7		N9

We still have two more pentominoes to consider. Starting from the third pentomino above we get five different hexominoes. There are other locations where we could place a green square, but they are all congruent to one of the five hexominoes shown.


		N3	N10

We can rule out the first three easily. The first contains a square of four squares; the second includes one of the pentominoes that does not fold into a box. The third has two extra squares on the same side. We need to check the last two more carefully. First we want to see if they are congruent to any of the “approved” nets. The fourth hexomino is congruent to N3. (If you rotate N3 90 degrees to the right, it matches the fourth hexomino.)

The last hexomino, N10, is not congruent to any of the others we’ve looked at yet. So we test it by cutting and folding. It works, giving us our tenth net.

There is one more pentomino to check—the last of the four remaining pentominoes shown above. This is the most complex one of all, producing ten non-congruent hexominoes that we have to check. Let's label them H1–H10 and see which ones can be ruled out quickly.


H1	H2	H3	H4	H5

H6	H7	H8	H9	H10

N11

H1, H2, H6, and H7 can be ruled out because they include pentominoes that don’t make a box. H3 can be ruled out because it contains a strip of four squares with two squares on one side of the strip. This leaves H4, H5, H8, H9, and H10 to be examined. First we’ll check to see if they are congruent to any we’ve already tested. H4 is not like any of the ones we’ve already seen. H5 is congruent to one of the hexominoes that doesn’t work. H8, H9, and H10 are congruent to N10, N7, and N8, respectively.

This leaves H4 for testing by cutting and folding. It works. So we have one more solution. H4 becomes our final net, N11.

Math Puzzle

Or log in with...

Puzzle

Boxes, Cubes, and Nets

Puzzle 1

Puzzle 1

Follow Hootsgo

Choose a topic

Quick Links

Communities

Subjects

Roles

About Hootsgo

Search form

Or log in with...

Puzzle

Boxes, Cubes, and Nets

Puzzle 1

Puzzle 1

Follow Hootsgo

Choose a topic

Quick Links

Communities

Subjects

Roles

About Hootsgo