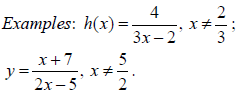| |
Content |
Further guidance |
Links |
| 2.1 |
- Concept of function f : x--> f (x).
- Domain, range; image (value).
- Composite functions.
- Identity function. Inverse function f-1
Not required:
|
 - On examination papers, students will only be asked to find the inverse of a one-to-one function.
|
- Int: The development of functions, Rene Descartes (France), Gottfried Wilhelm Leibniz (Germany) and Leonhard Euler (Switzerland).
- TOK: Is zero the same as “nothing”?
- TOK: Is mathematics a formal language?
|
| 2.2 |
- The graph of a function; its equation y = f (x).
- Function graphing skills.
- Investigation of key features of graphs, such as maximum and minimum values, intercepts,horizontal and vertical asymptotes, symmetry,and consideration of domain and range.
- Use of technology to graph a variety of functions, including ones not specifically mentioned.
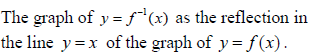
|
- Note the difference in the command terms “draw” and “sketch”.
- An analytic approach is also expected for simple functions, including all those listed under topic 2.
- Link to 6.3, local maximum and minimum points.
|
- Appl: Chemistry 11.3.1 (sketching and interpreting graphs); geographic skills.
- TOK: How accurate is a visual representation of a mathematical concept? (Limits of graphs in delivering information about functions and phenomena in general, relevance of modes of representation.)
|
| 2.3 |
- Transformations of graphs.
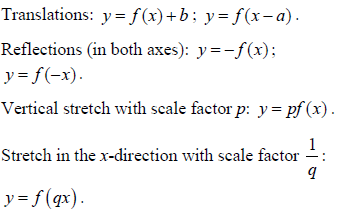 - Composite transformations.
|
- Technology should be used to investigate these transformations.
- Translation by the vector
 denotes horizontal shift of 3 units to the right, and vertical shift of 2 down. denotes horizontal shift of 3 units to the right, and vertical shift of 2 down.
- Example:y = x2 used to obtain y = 3x2 + 2 by a stretch of scale factor 3 in the y-direction followed by a translation of
 . .
|
Appl: Economics 1.1 (shifting of supply and demand curves). |
| 2.4 |
|
- Candidates are expected to be able to change from one form to another.
- Links to 2.3, transformations; 2.7, quadratic equations.
|
- Appl: Chemistry 17.2 (equilibrium law).
- Appl: Physics 2.1 (kinematics).
- Appl: Physics 4.2 (simple harmonic motion).
- Appl: Physics 9.1 (HL only) (projectile motion).
|
| 2.5 |
- The reciprocal function
 its graph and self-inverse nature. its graph and self-inverse nature.
- The rational function
 and its graph. and its graph.
- Vertical and horizontal asymptotes.
|
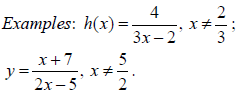
Diagrams should include all asymptotes and intercepts.
|
|
| 2.6 |
|
Links to 1.1, geometric sequences; 1.2, laws of exponents and logarithms; 2.1, inverse functions; 2.2, graphs of inverses; and 6.1, limits. |
Int: The Babylonian method of multiplication:  Sulba Sutras in ancient 2 India and the Bakhshali Manuscript contained an algebraic formula for solving quadratic equations. Sulba Sutras in ancient 2 India and the Bakhshali Manuscript contained an algebraic formula for solving quadratic equations. |
| 2.7 |
- Solving equations, both graphically and analytically.
- Use of technology to solve a variety of equations, including those where there is no appropriate analytic approach.
- Solving ax2 + bx + c = 0 , a ≠ 0 ..
- The quadratic formula.
- The discriminantand Δ = b2 − 4ac the nature of the roots, that is, two distinct real roots, two equal real roots, no real roots.
- Solving exponential equations.
|
- Solutions may be referred to as roots of equations or zeros of functions.
- Links to 2.2, function graphing skills; and 2.3– 2.6, equations involving specific functions.
- Examples:ex = sin x, x4 + 5x − 6 = 0 .
- Example: Find k given that the equation has two equal real roots.
- Examples:

- Link to 1.2, exponents and logarithms.
|
. |
| 2.8 |
Applications of graphing skills and solving equations that relate to real-life situations. |
Link to 1.1, geometric series. |
- Appl: Compound interest, growth and decay; projectile motion; braking distance; electrical circuits.
- Appl: Physics 7.2.7–7.2.9, 13.2.5, 13.2.6,13.2.8 Physics,(radioactive decay and half-life)
|
 Sulba Sutras in ancient 2 India and the Bakhshali Manuscript contained an algebraic formula for solving quadratic equations.
Sulba Sutras in ancient 2 India and the Bakhshali Manuscript contained an algebraic formula for solving quadratic equations.


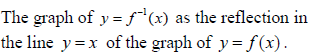
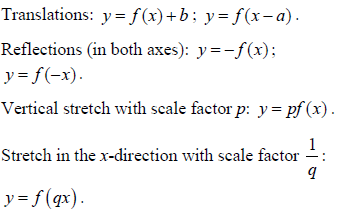
 denotes horizontal shift of 3 units to the right, and vertical shift of 2 down.
denotes horizontal shift of 3 units to the right, and vertical shift of 2 down. .
.
 its graph and self-inverse nature.
its graph and self-inverse nature. and its graph.
and its graph.